
Question Number 125034 by mathmax by abdo last updated on 07/Dec/20
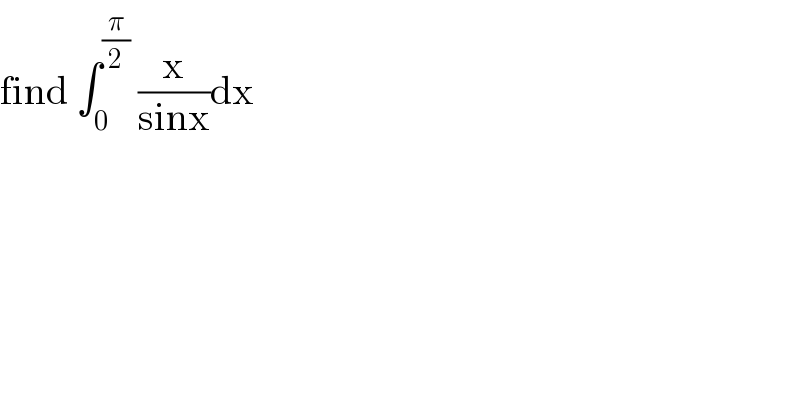
$$\mathrm{find}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{x}}{\mathrm{sinx}}\mathrm{dx} \\ $$
Commented by Olaf last updated on 07/Dec/20
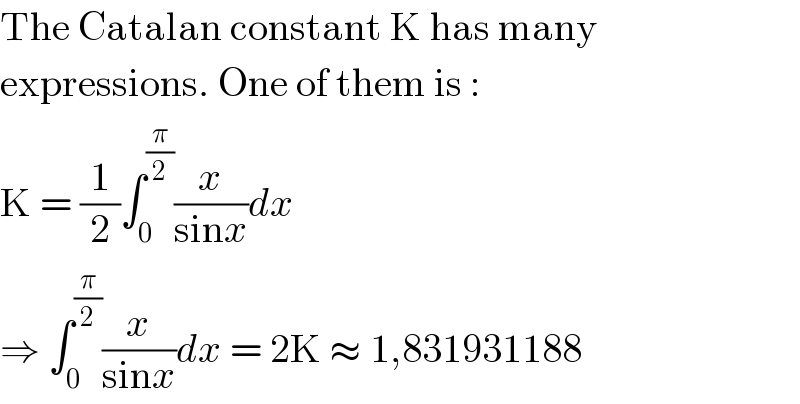
$$\mathrm{The}\:\mathrm{Catalan}\:\mathrm{constant}\:\mathrm{K}\:\mathrm{has}\:\mathrm{many} \\ $$$$\mathrm{expressions}.\:\mathrm{One}\:\mathrm{of}\:\mathrm{them}\:\mathrm{is}\:: \\ $$$$\mathrm{K}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}}{\mathrm{sin}{x}}{dx} \\ $$$$\Rightarrow\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}}{\mathrm{sin}{x}}{dx}\:=\:\mathrm{2K}\:\approx\:\mathrm{1},\mathrm{831931188} \\ $$
