
Question Number 124931 by ZiYangLee last updated on 07/Dec/20

$$\mathrm{If}\:\mathrm{3}^{\mathrm{2019}} +{k}\:\mathrm{is}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{11},\: \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{positive}\:\mathrm{integer}\:{k}. \\ $$
Answered by MJS_new last updated on 07/Dec/20
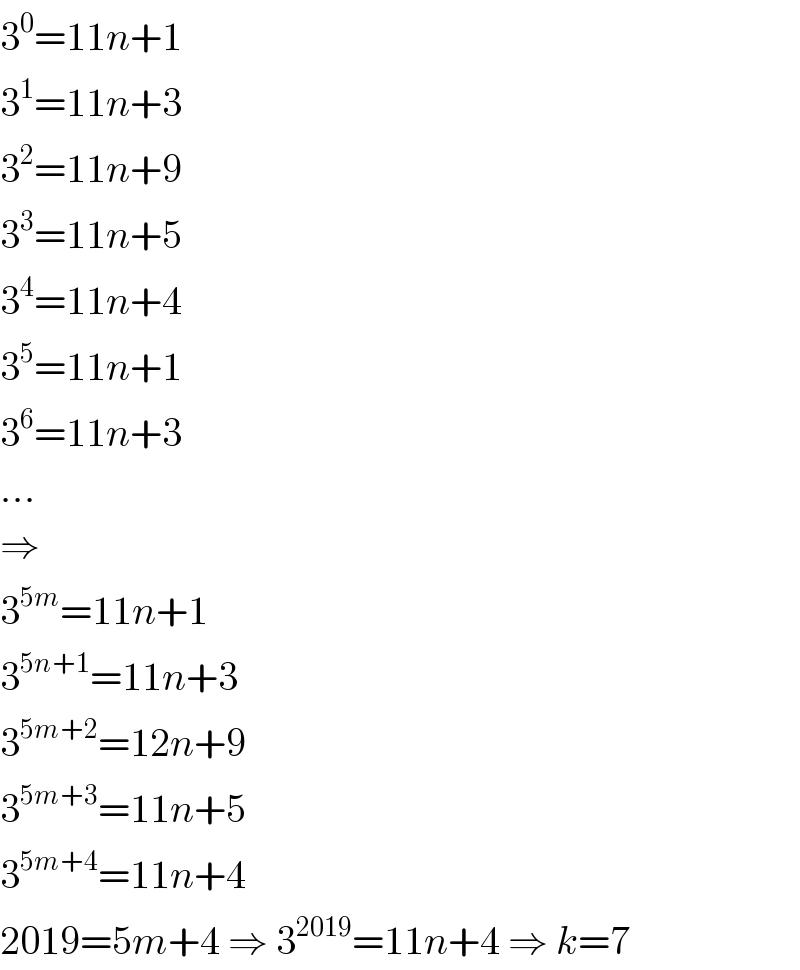
$$\mathrm{3}^{\mathrm{0}} =\mathrm{11}{n}+\mathrm{1} \\ $$$$\mathrm{3}^{\mathrm{1}} =\mathrm{11}{n}+\mathrm{3} \\ $$$$\mathrm{3}^{\mathrm{2}} =\mathrm{11}{n}+\mathrm{9} \\ $$$$\mathrm{3}^{\mathrm{3}} =\mathrm{11}{n}+\mathrm{5} \\ $$$$\mathrm{3}^{\mathrm{4}} =\mathrm{11}{n}+\mathrm{4} \\ $$$$\mathrm{3}^{\mathrm{5}} =\mathrm{11}{n}+\mathrm{1} \\ $$$$\mathrm{3}^{\mathrm{6}} =\mathrm{11}{n}+\mathrm{3} \\ $$$$... \\ $$$$\Rightarrow \\ $$$$\mathrm{3}^{\mathrm{5}{m}} =\mathrm{11}{n}+\mathrm{1} \\ $$$$\mathrm{3}^{\mathrm{5}{n}+\mathrm{1}} =\mathrm{11}{n}+\mathrm{3} \\ $$$$\mathrm{3}^{\mathrm{5}{m}+\mathrm{2}} =\mathrm{12}{n}+\mathrm{9} \\ $$$$\mathrm{3}^{\mathrm{5}{m}+\mathrm{3}} =\mathrm{11}{n}+\mathrm{5} \\ $$$$\mathrm{3}^{\mathrm{5}{m}+\mathrm{4}} =\mathrm{11}{n}+\mathrm{4} \\ $$$$\mathrm{2019}=\mathrm{5}{m}+\mathrm{4}\:\Rightarrow\:\mathrm{3}^{\mathrm{2019}} =\mathrm{11}{n}+\mathrm{4}\:\Rightarrow\:{k}=\mathrm{7} \\ $$
