
Question Number 124928 by bemath last updated on 07/Dec/20
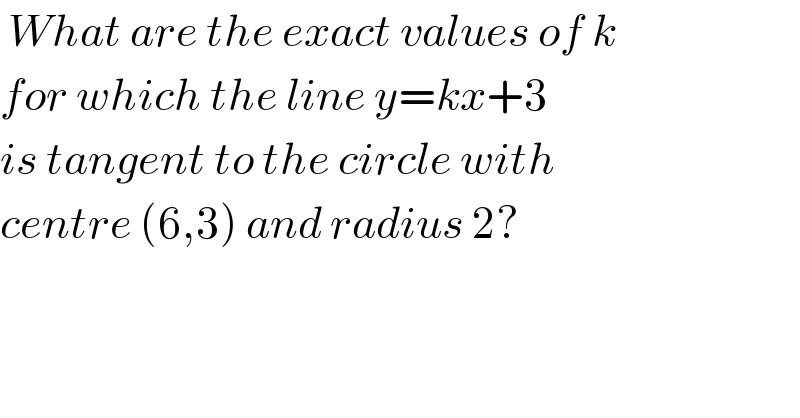
$$\:{What}\:{are}\:{the}\:{exact}\:{values}\:{of}\:{k} \\ $$$${for}\:{which}\:{the}\:{line}\:{y}={kx}+\mathrm{3} \\ $$$${is}\:{tangent}\:{to}\:{the}\:{circle}\:{with} \\ $$$${centre}\:\left(\mathrm{6},\mathrm{3}\right)\:{and}\:{radius}\:\mathrm{2}? \\ $$
Answered by mr W last updated on 07/Dec/20

$$\mathrm{2}=\frac{\mathrm{6}{k}−\mathrm{3}+\mathrm{3}}{\:\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$\mathrm{8}{k}^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow{k}=\pm\frac{\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$
