
Previous in Differential Equation Next in Differential Equation
Question Number 124923 by bemath last updated on 07/Dec/20
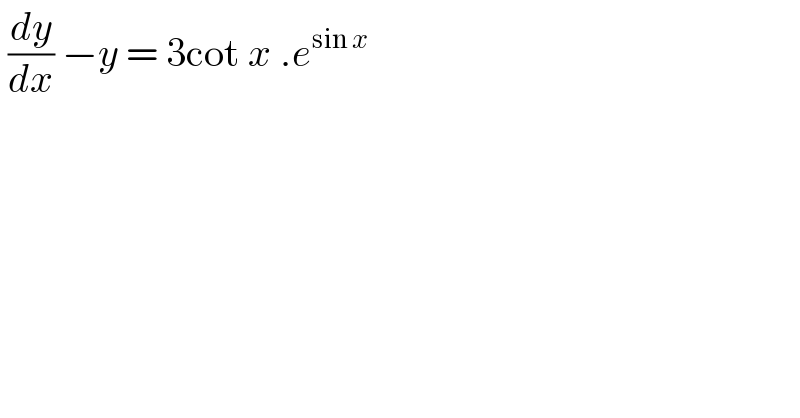
$$\:\frac{{dy}}{{dx}}\:−{y}\:=\:\mathrm{3cot}\:{x}\:.{e}^{\mathrm{sin}\:{x}} \: \\ $$$$ \\ $$
Commented by mohammad17 last updated on 07/Dec/20
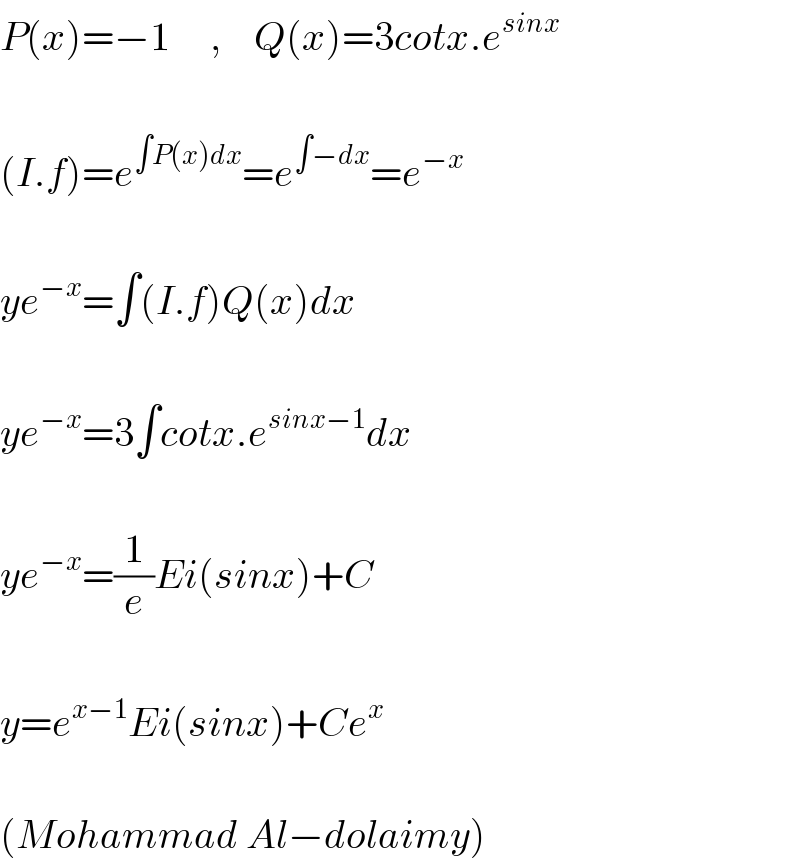
$${P}\left({x}\right)=−\mathrm{1}\:\:\:\:\:,\:\:\:\:{Q}\left({x}\right)=\mathrm{3}{cotx}.{e}^{{sinx}} \\ $$$$ \\ $$$$\left({I}.{f}\right)={e}^{\int{P}\left({x}\right){dx}} ={e}^{\int−{dx}} ={e}^{−{x}} \\ $$$$ \\ $$$${ye}^{−{x}} =\int\left({I}.{f}\right){Q}\left({x}\right){dx} \\ $$$$ \\ $$$${ye}^{−{x}} =\mathrm{3}\int{cotx}.{e}^{{sinx}−\mathrm{1}} {dx} \\ $$$$ \\ $$$${ye}^{−{x}} =\frac{\mathrm{1}}{{e}}{Ei}\left({sinx}\right)+{C} \\ $$$$ \\ $$$${y}={e}^{{x}−\mathrm{1}} {Ei}\left({sinx}\right)+{Ce}^{{x}} \\ $$$$ \\ $$$$\left({Mohammad}\:{Al}−{dolaimy}\right) \\ $$
