
Question Number 124819 by Ndala last updated on 06/Dec/20
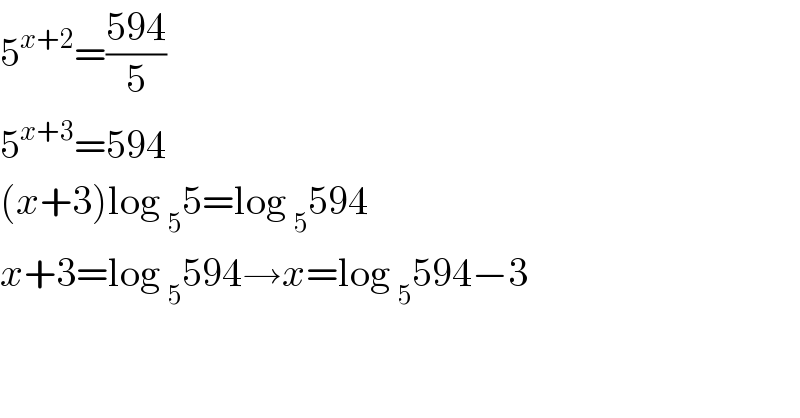
$$\mathrm{5}^{{x}+\mathrm{2}} =\frac{\mathrm{594}}{\mathrm{5}} \\ $$$$\mathrm{5}^{{x}+\mathrm{3}} =\mathrm{594} \\ $$$$\left({x}+\mathrm{3}\right)\mathrm{log}\:_{\mathrm{5}} \mathrm{5}=\mathrm{log}\:_{\mathrm{5}} \mathrm{594} \\ $$$${x}+\mathrm{3}=\mathrm{log}\:_{\mathrm{5}} \mathrm{594}\rightarrow{x}=\mathrm{log}\:_{\mathrm{5}} \mathrm{594}−\mathrm{3} \\ $$
Commented by $@y@m last updated on 06/Dec/20

$${Please}\:{use}\:{editor}\:{option}\:\left({available}\right. \\ $$$$\left.{under}\:\equiv\right)\:{for}\:{rough}\:{work}. \\ $$
