
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 124709 by benjo_mathlover last updated on 05/Dec/20
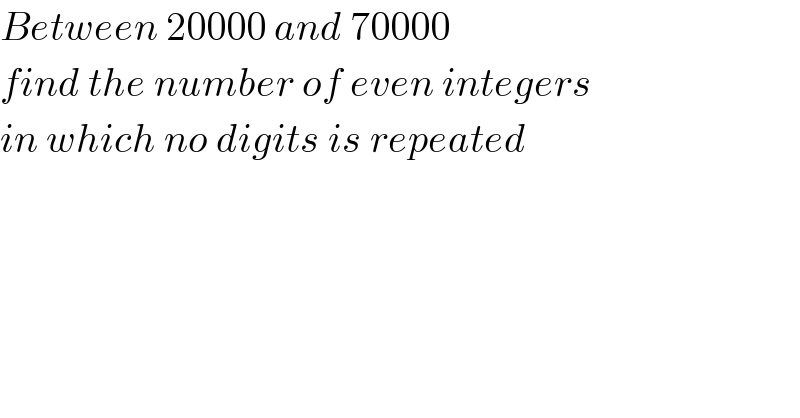
$${Between}\:\mathrm{20000}\:{and}\:\mathrm{70000}\: \\ $$$${find}\:{the}\:{number}\:{of}\:{even}\:{integers} \\ $$$${in}\:{which}\:{no}\:{digits}\:{is}\:{repeated} \\ $$
Answered by liberty last updated on 05/Dec/20

$${Let}\:{abcde}\:{be}\:{a}\:{required}\:{even}\:{integer}.\: \\ $$$${As}\:{shown}\:{in}\:{the}\:{following}\:{diagram},\:{the} \\ $$$$\mathrm{1}^{{st}} \:{digit}\:{can}\:{be}\:{chosen}\:{from}\:\left\{\:\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6}\right\} \\ $$$${and}\:{the}\:\mathrm{5}^{{th}} \:{digit}\:{e}\:{can}\:{be}\:{chosen}\:{from}\: \\ $$$$\left\{\mathrm{0},\mathrm{2},\mathrm{4},\mathrm{6},\mathrm{8}\right\}. \\ $$$$\:\lfloor\:\:{a}\:\rfloor\:\lfloor\:{b}\:{c}\:{d}\:\rfloor\:\lfloor{e}\:\rfloor\: \\ $$$${since}\:\left\{\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6}\right\}\:\cap\:\left\{\:\mathrm{0},\mathrm{2},\mathrm{4},\mathrm{6},\mathrm{8}\right\}=\:\left\{\mathrm{2},\mathrm{4},\mathrm{6}\right\} \\ $$$${we}\:{devide}\:{the}\:{problem}\:{into}\:\mathrm{2}\:{disjoint}\:{cases} \\ $$$${case}\left(\mathrm{1}\right)\:{a}\:\in\:\left\{\mathrm{2},\mathrm{4},\mathrm{6}\right\}\:{there}\:{are}\:=\:\mathrm{3}×\mathrm{4}×{P}\:_{\mathrm{3}} ^{\mathrm{8}} \\ $$$${case}\left(\mathrm{2}\right)\:{a}\:\in\:\left\{\mathrm{3},\mathrm{5}\right\}\:{there}\:{are}\:=\:\mathrm{2}×\mathrm{5}×{P}\:_{\mathrm{3}} ^{\mathrm{8}} \\ $$$${The}\:{total}\:{number}\:{of}\:{required}\:{even}\:{numbers} \\ $$$${is}\:\mathrm{4032}\:+\:\mathrm{3360}\:=\:\mathrm{7392}\:. \\ $$
Answered by mr W last updated on 06/Dec/20
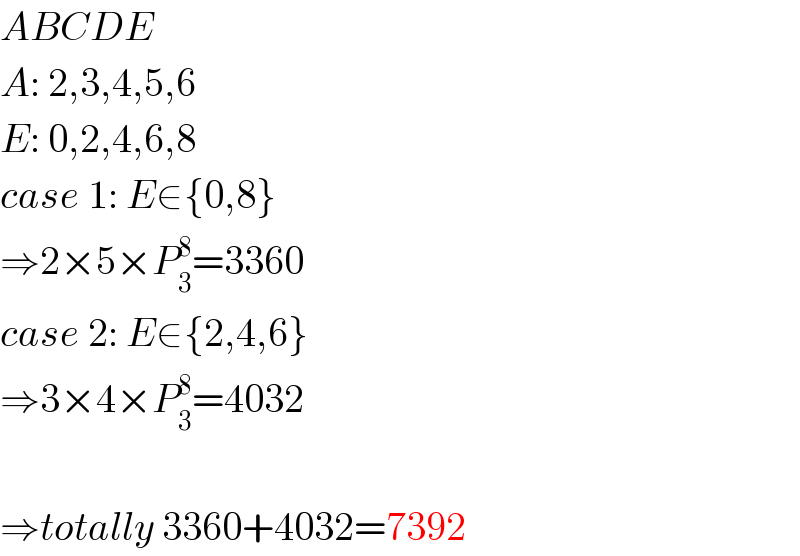
$${ABCDE} \\ $$$${A}:\:\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5},\mathrm{6} \\ $$$${E}:\:\mathrm{0},\mathrm{2},\mathrm{4},\mathrm{6},\mathrm{8} \\ $$$${case}\:\mathrm{1}:\:{E}\in\left\{\mathrm{0},\mathrm{8}\right\} \\ $$$$\Rightarrow\mathrm{2}×\mathrm{5}×{P}_{\mathrm{3}} ^{\mathrm{8}} =\mathrm{3360} \\ $$$${case}\:\mathrm{2}:\:{E}\in\left\{\mathrm{2},\mathrm{4},\mathrm{6}\right\} \\ $$$$\Rightarrow\mathrm{3}×\mathrm{4}×{P}_{\mathrm{3}} ^{\mathrm{8}} =\mathrm{4032} \\ $$$$ \\ $$$$\Rightarrow{totally}\:\mathrm{3360}+\mathrm{4032}=\mathrm{7392} \\ $$
