
Question Number 124594 by physicstutes last updated on 04/Dec/20
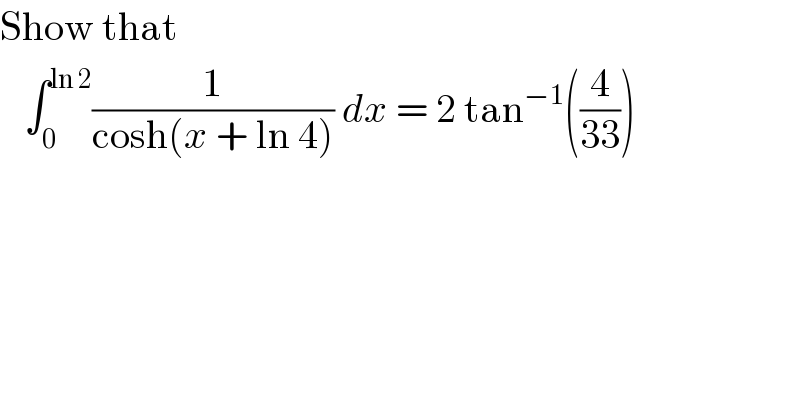
$$\mathrm{Show}\:\mathrm{that}\: \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\mathrm{ln}\:\mathrm{2}} \frac{\mathrm{1}}{\mathrm{cosh}\left({x}\:+\:\mathrm{ln}\:\mathrm{4}\right)}\:{dx}\:=\:\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{33}}\right) \\ $$
Commented by mohammad17 last updated on 04/Dec/20
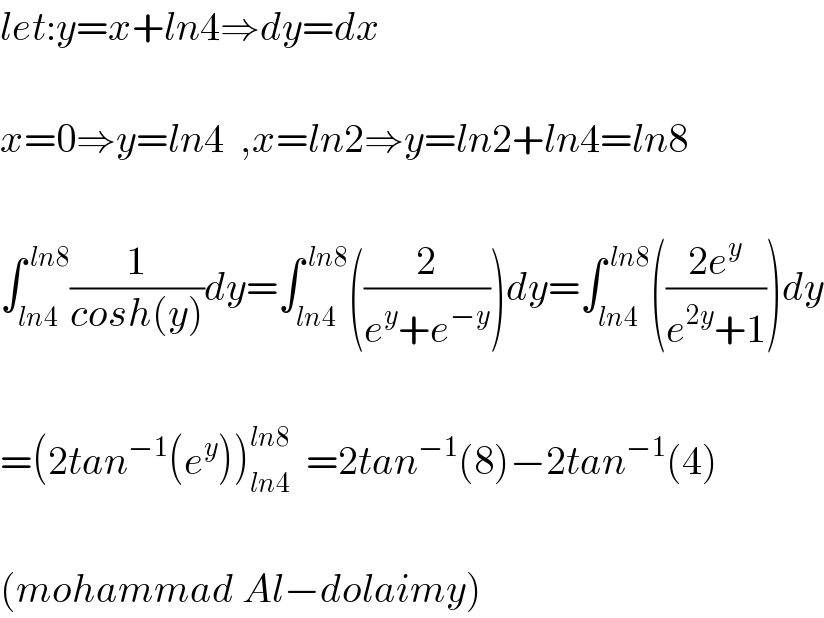
$${let}:{y}={x}+{ln}\mathrm{4}\Rightarrow{dy}={dx} \\ $$$$ \\ $$$${x}=\mathrm{0}\Rightarrow{y}={ln}\mathrm{4}\:\:,{x}={ln}\mathrm{2}\Rightarrow{y}={ln}\mathrm{2}+{ln}\mathrm{4}={ln}\mathrm{8} \\ $$$$ \\ $$$$\int_{{ln}\mathrm{4}} ^{\:{ln}\mathrm{8}} \frac{\mathrm{1}}{{cosh}\left({y}\right)}{dy}=\int_{{ln}\mathrm{4}} ^{\:{ln}\mathrm{8}} \left(\frac{\mathrm{2}}{{e}^{{y}} +{e}^{−{y}} }\right){dy}=\int_{{ln}\mathrm{4}} ^{\:{ln}\mathrm{8}} \left(\frac{\mathrm{2}{e}^{{y}} }{{e}^{\mathrm{2}{y}} +\mathrm{1}}\right){dy} \\ $$$$ \\ $$$$=\left(\mathrm{2}{tan}^{−\mathrm{1}} \left({e}^{{y}} \right)\right)_{{ln}\mathrm{4}} ^{{ln}\mathrm{8}} \:\:=\mathrm{2}{tan}^{−\mathrm{1}} \left(\mathrm{8}\right)−\mathrm{2}{tan}^{−\mathrm{1}} \left(\mathrm{4}\right) \\ $$$$ \\ $$$$\left({mohammad}\:{Al}−{dolaimy}\right) \\ $$
Answered by Ar Brandon last updated on 04/Dec/20
![I=∫_0 ^(ln2) (1/(cosh(x+ln4)))dx x+ln4=u ⇒ dx=du I=∫_(ln4) ^(ln8) (du/(cosh(u)))=∫_(ln4) ^(ln8) (du/((1/2)(e^u +e^(−u) ))) =2∫_(ln4) ^(ln8) ((e^u du)/(e^(2u) +1))=2∫_4 ^8 (dt/(t^2 +1))=2[tan^(−1) (t)]_4 ^8 =2[tan^(−1) (8)−tan^(−1) (4)]](Q124604.png)
$$\mathcal{I}=\int_{\mathrm{0}} ^{\mathrm{ln2}} \frac{\mathrm{1}}{\mathrm{cosh}\left(\mathrm{x}+\mathrm{ln4}\right)}\mathrm{dx} \\ $$$$\mathrm{x}+\mathrm{ln4}=\mathrm{u}\:\Rightarrow\:\mathrm{dx}=\mathrm{du} \\ $$$$\mathcal{I}=\int_{\mathrm{ln4}} ^{\mathrm{ln8}} \frac{\mathrm{du}}{\mathrm{cosh}\left(\mathrm{u}\right)}=\int_{\mathrm{ln4}} ^{\mathrm{ln8}} \frac{\mathrm{du}}{\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{e}^{\mathrm{u}} +\mathrm{e}^{−\mathrm{u}} \right)} \\ $$$$\:\:\:=\mathrm{2}\int_{\mathrm{ln4}} ^{\mathrm{ln8}} \frac{\mathrm{e}^{\mathrm{u}} \mathrm{du}}{\mathrm{e}^{\mathrm{2u}} +\mathrm{1}}=\mathrm{2}\int_{\mathrm{4}} ^{\mathrm{8}} \frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{2}\left[\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{t}\right)\right]_{\mathrm{4}} ^{\mathrm{8}} \\ $$$$\:\:\:=\mathrm{2}\left[\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{8}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{4}\right)\right] \\ $$
