
Previous in Relation and Functions Next in Relation and Functions
Question Number 124580 by Boucatchou last updated on 04/Dec/20
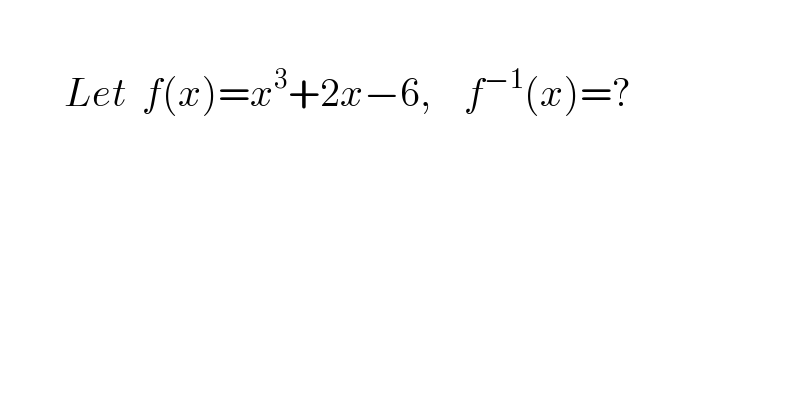
$$ \\ $$$$\:\:\:\:\:\:\:\:{Let}\:\:{f}\left({x}\right)={x}^{\mathrm{3}} +\mathrm{2}{x}−\mathrm{6},\:\:\:\:{f}^{−\mathrm{1}} \left({x}\right)=? \\ $$
Answered by MJS_new last updated on 04/Dec/20
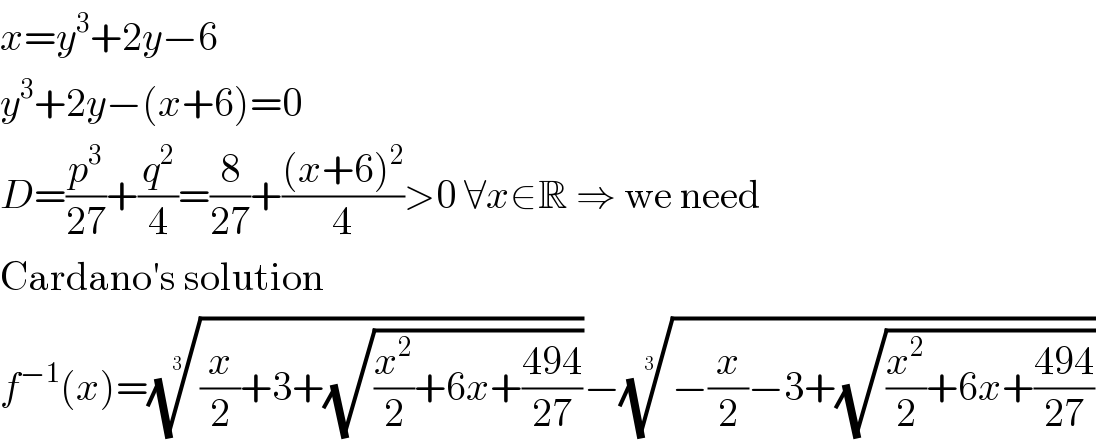
$${x}={y}^{\mathrm{3}} +\mathrm{2}{y}−\mathrm{6} \\ $$$${y}^{\mathrm{3}} +\mathrm{2}{y}−\left({x}+\mathrm{6}\right)=\mathrm{0} \\ $$$${D}=\frac{{p}^{\mathrm{3}} }{\mathrm{27}}+\frac{{q}^{\mathrm{2}} }{\mathrm{4}}=\frac{\mathrm{8}}{\mathrm{27}}+\frac{\left({x}+\mathrm{6}\right)^{\mathrm{2}} }{\mathrm{4}}>\mathrm{0}\:\forall{x}\in\mathbb{R}\:\Rightarrow\:\mathrm{we}\:\mathrm{need} \\ $$$$\mathrm{Cardano}'\mathrm{s}\:\mathrm{solution} \\ $$$${f}^{−\mathrm{1}} \left({x}\right)=\sqrt[{\mathrm{3}}]{\frac{{x}}{\mathrm{2}}+\mathrm{3}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{6}{x}+\frac{\mathrm{494}}{\mathrm{27}}}}−\sqrt[{\mathrm{3}}]{−\frac{{x}}{\mathrm{2}}−\mathrm{3}+\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{6}{x}+\frac{\mathrm{494}}{\mathrm{27}}}} \\ $$
