
Question Number 124579 by bemath last updated on 04/Dec/20
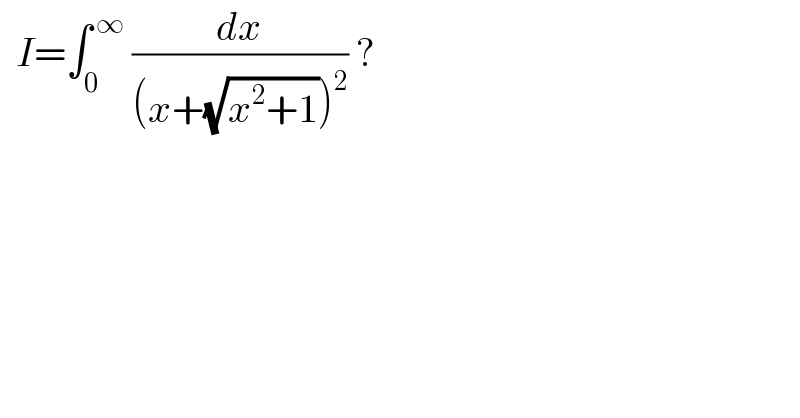
$$\:\:{I}=\int_{\mathrm{0}} ^{\:\infty} \:\frac{{dx}}{\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }\:? \\ $$
Answered by liberty last updated on 04/Dec/20
![I=∫_( 0) ^( ∞) (dx/((x+(√(x^2 +1)))^2 )) letting cot 2β = x →dx = −2cosec^2 β dβ the integral becomes I=∫_(π/4) ^( 0) ((−2cosec^2 2β dβ)/((cot 2β+cosec 2β)^2 )) I=∫_(0 ) ^( π/4) (1/((cos 2β+1)^2 )) dβ = (1/2)∫_0 ^( π/4) (dβ/(cos^4 β)) I=(1/2)∫_0 ^( π/4) sec^2 β(tan^2 β+1) dβ I= (1/2) [ ((tan^3 β)/3)+tan β ]_( 0) ^(π/4) = (2/3)](Q124581.png)
$${I}=\int_{\:\mathrm{0}} ^{\:\infty} \:\frac{{dx}}{\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$\:{letting}\:\mathrm{cot}\:\mathrm{2}\beta\:=\:{x}\:\rightarrow{dx}\:=\:−\mathrm{2cosec}\:^{\mathrm{2}} \beta\:{d}\beta \\ $$$${the}\:{integral}\:{becomes}\: \\ $$$${I}=\int_{\pi/\mathrm{4}} ^{\:\mathrm{0}} \frac{−\mathrm{2cosec}\:^{\mathrm{2}} \mathrm{2}\beta\:{d}\beta}{\left(\mathrm{cot}\:\mathrm{2}\beta+\mathrm{cosec}\:\mathrm{2}\beta\right)^{\mathrm{2}} } \\ $$$${I}=\underset{\mathrm{0}\:} {\overset{\:\pi/\mathrm{4}} {\int}}\frac{\mathrm{1}}{\left(\mathrm{cos}\:\mathrm{2}\beta+\mathrm{1}\right)^{\mathrm{2}} }\:{d}\beta\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\:\pi/\mathrm{4}} {\int}}\:\frac{{d}\beta}{\mathrm{cos}\:^{\mathrm{4}} \beta} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\:\pi/\mathrm{4}} {\int}}\:\mathrm{sec}\:^{\mathrm{2}} \beta\left(\mathrm{tan}\:^{\mathrm{2}} \beta+\mathrm{1}\right)\:{d}\beta \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:\frac{\mathrm{tan}\:^{\mathrm{3}} \beta}{\mathrm{3}}+\mathrm{tan}\:\beta\:\right]_{\:\mathrm{0}} ^{\pi/\mathrm{4}} =\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Commented by peter frank last updated on 05/Dec/20

$$\mathrm{thanks} \\ $$
Answered by Bird last updated on 04/Dec/20
![I=∫_0 ^∞ (dx/((x+(√(x^2 +1)))^2 )) we do the changement x=sht ⇒I=∫_0 ^∞ ((cht)/((sht+cht)^2 ))dt =∫_0 ^∞ ((cht)/((((e^t −e^(−t) )/2)+((e^t −e^(−t) )/2))^2 ))dt =∫_0 ^∞ e^(−2t) (((e^t +e^(−t) )/2))dt =(1/2)∫_0 ^∞ (e^(−t ) +e^(−3t) )dt =(1/2)[−e^(−t) −(1/3)e^(−3t) ]_0 ^(+∞) =(1/2)( 1+(1/3))=(1/2)((4/3))=(2/3)](Q124582.png)
$${I}=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dx}}{\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }\:{we}\:{do}\:{the}\:{changement} \\ $$$${x}={sht}\:\Rightarrow{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{{cht}}{\left({sht}+{cht}\right)^{\mathrm{2}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cht}}{\left(\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}+\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}\right)^{\mathrm{2}} }{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} \left(\frac{{e}^{{t}} +{e}^{−{t}} }{\mathrm{2}}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\left({e}^{−{t}\:} +{e}^{−\mathrm{3}{t}} \right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−{e}^{−{t}} −\frac{\mathrm{1}}{\mathrm{3}}{e}^{−\mathrm{3}{t}} \right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$ \\ $$
Answered by Dwaipayan Shikari last updated on 04/Dec/20
![As per previous result I=[−(1/(6(x+(√(x^2 +1)))^3 ))−(1/(2(x+(√(x^2 +1)))))]_0 ^∞ =(1/6)+(1/2)=(2/3)](Q124583.png)
$${As}\:{per}\:\:{previous}\:{result}\: \\ $$$${I}=\left[−\frac{\mathrm{1}}{\mathrm{6}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{2}\left({x}+\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}\right)}\right]_{\mathrm{0}} ^{\infty} =\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by Ar Brandon last updated on 04/Dec/20
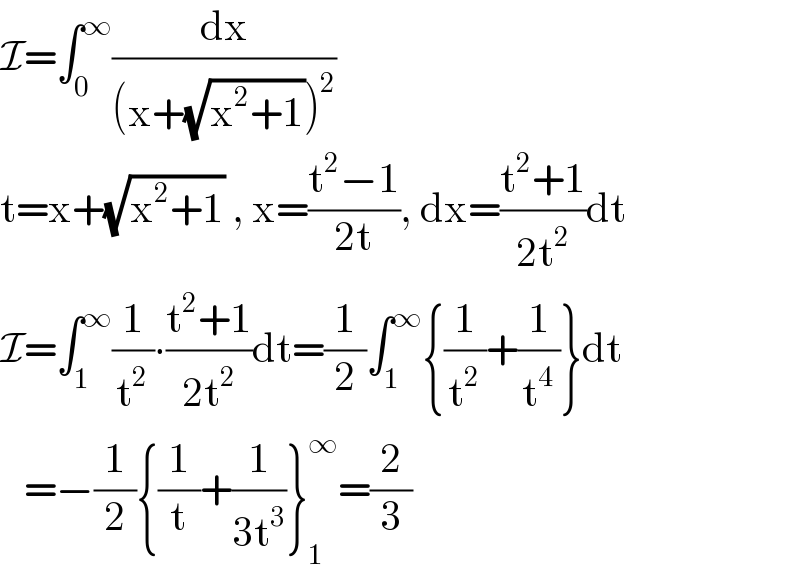
$$\mathcal{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{t}=\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\:,\:\mathrm{x}=\frac{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2t}},\:\mathrm{dx}=\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathcal{I}=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }\centerdot\frac{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2t}^{\mathrm{2}} }\mathrm{dt}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{1}} ^{\infty} \left\{\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{t}^{\mathrm{4}} }\right\}\mathrm{dt} \\ $$$$\:\:\:=−\frac{\mathrm{1}}{\mathrm{2}}\left\{\frac{\mathrm{1}}{\mathrm{t}}+\frac{\mathrm{1}}{\mathrm{3t}^{\mathrm{3}} }\right\}_{\mathrm{1}} ^{\infty} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$
Answered by Ar Brandon last updated on 04/Dec/20

$$\mathcal{I}=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\left(\mathrm{x}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{x}=\mathrm{tan}\theta\:\Rightarrow\:\mathrm{dx}=\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\mathcal{I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta}{\left(\mathrm{tan}\theta+\sqrt{\mathrm{tan}^{\mathrm{2}} \theta+\mathrm{1}}\right)^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta}{\left(\mathrm{tan}\theta+\mathrm{sec}\theta\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{d}\theta}{\left(\mathrm{sin}\theta+\mathrm{1}\right)^{\mathrm{2}} }=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(\mathrm{1}−\mathrm{sin}\theta\right)^{\mathrm{2}} }{\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \theta\right)^{\mathrm{2}} }\mathrm{d}\theta \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left\{\frac{\mathrm{1}−\mathrm{2sin}\theta+\mathrm{sin}^{\mathrm{2}} \theta}{\mathrm{cos}^{\mathrm{4}} \theta}\right\}\mathrm{d}\theta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left\{\frac{\mathrm{cos}^{\mathrm{2}} \theta−\mathrm{2sin}\theta+\mathrm{2sin}^{\mathrm{2}} \theta}{\mathrm{cos}^{\mathrm{4}} \theta}\right\}\mathrm{d}\theta \\ $$$$\:\:\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left(−\mathrm{sin}\theta\right)}{\mathrm{cos}^{\mathrm{4}} \theta}\mathrm{d}\theta+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{tan}^{\mathrm{2}} \theta\mathrm{sec}^{\mathrm{2}} \theta\mathrm{d}\theta \\ $$$$\:\:\:=\left\{\mathrm{tan}\theta−\frac{\mathrm{2}}{\mathrm{3cos}^{\mathrm{3}} \theta}+\frac{\mathrm{2tan}^{\mathrm{3}} \theta}{\mathrm{3}}\right\}_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} =\frac{\mathrm{2}}{\mathrm{3}} \\ $$
