
Question Number 124474 by sogol last updated on 03/Dec/20
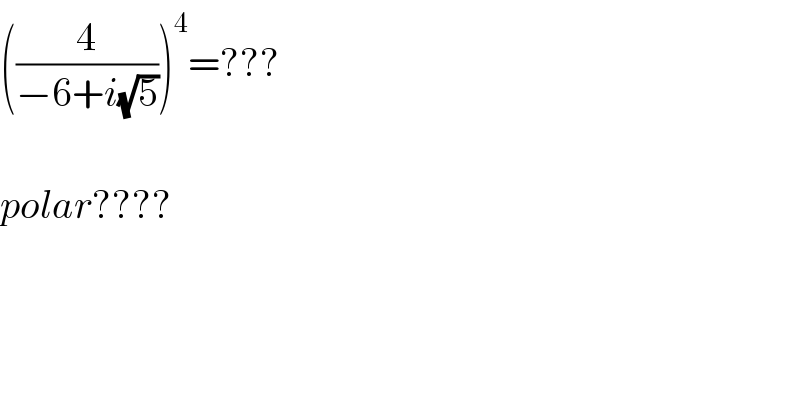
$$\left(\frac{\mathrm{4}}{−\mathrm{6}+{i}\sqrt{\mathrm{5}}}\right)^{\mathrm{4}} =??? \\ $$$$ \\ $$$${polar}???? \\ $$
Commented by MJS_new last updated on 03/Dec/20
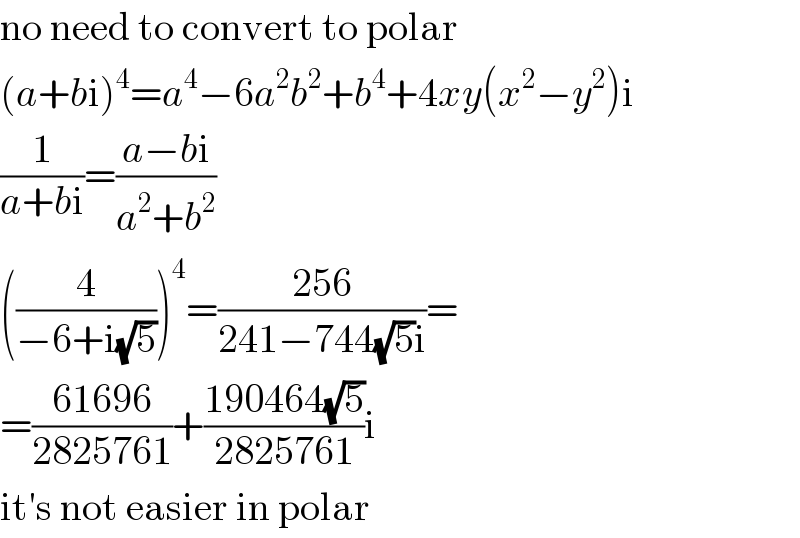
$$\mathrm{no}\:\mathrm{need}\:\mathrm{to}\:\mathrm{convert}\:\mathrm{to}\:\mathrm{polar} \\ $$$$\left({a}+{b}\mathrm{i}\right)^{\mathrm{4}} ={a}^{\mathrm{4}} −\mathrm{6}{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{4}} +\mathrm{4}{xy}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)\mathrm{i} \\ $$$$\frac{\mathrm{1}}{{a}+{b}\mathrm{i}}=\frac{{a}−{b}\mathrm{i}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$\left(\frac{\mathrm{4}}{−\mathrm{6}+\mathrm{i}\sqrt{\mathrm{5}}}\right)^{\mathrm{4}} =\frac{\mathrm{256}}{\mathrm{241}−\mathrm{744}\sqrt{\mathrm{5}}\mathrm{i}}= \\ $$$$=\frac{\mathrm{61696}}{\mathrm{2825761}}+\frac{\mathrm{190464}\sqrt{\mathrm{5}}}{\mathrm{2825761}}\mathrm{i} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{easier}\:\mathrm{in}\:\mathrm{polar} \\ $$
Answered by mathmax by abdo last updated on 03/Dec/20
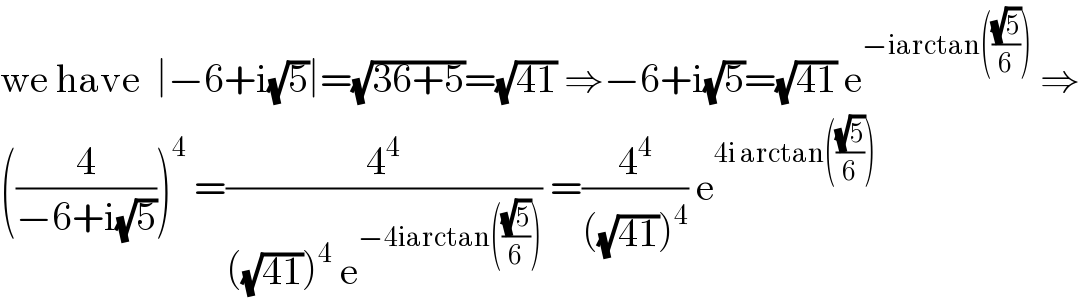
$$\mathrm{we}\:\mathrm{have}\:\:\mid−\mathrm{6}+\mathrm{i}\sqrt{\mathrm{5}}\mid=\sqrt{\mathrm{36}+\mathrm{5}}=\sqrt{\mathrm{41}}\:\Rightarrow−\mathrm{6}+\mathrm{i}\sqrt{\mathrm{5}}=\sqrt{\mathrm{41}}\:\mathrm{e}^{−\mathrm{iarctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{6}}\right)} \:\Rightarrow \\ $$$$\left(\frac{\mathrm{4}}{−\mathrm{6}+\mathrm{i}\sqrt{\mathrm{5}}}\right)^{\mathrm{4}} \:=\frac{\mathrm{4}^{\mathrm{4}} }{\left(\sqrt{\mathrm{41}}\right)^{\mathrm{4}} \:\mathrm{e}^{−\mathrm{4iarctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{6}}\right)} }\:=\frac{\mathrm{4}^{\mathrm{4}} }{\left(\sqrt{\mathrm{41}}\right)^{\mathrm{4}} }\:\mathrm{e}^{\mathrm{4i}\:\mathrm{arctan}\left(\frac{\sqrt{\mathrm{5}}}{\mathrm{6}}\right)} \\ $$
