
Question Number 124430 by benjo_mathlover last updated on 03/Dec/20
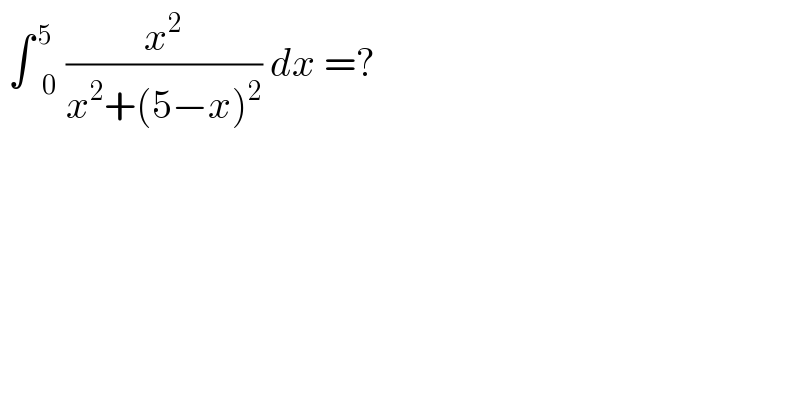
$$\:\int\overset{\:\mathrm{5}} {\:}_{\mathrm{0}} \frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\left(\mathrm{5}−{x}\right)^{\mathrm{2}} }\:{dx}\:=?\: \\ $$
Answered by liberty last updated on 03/Dec/20
![μ =∫_0 ^( 5) (x^2 /(x^2 +(5−x)^2 )) dx . [use the interval inverting substitution replacing x by 5−x ] μ =∫_5 ^( 0) (((5−x)^2 )/((5−x)^2 +x^2 )) (−dx)=∫_0 ^( 5) (((5−x)^2 )/(x^2 +(5−x)^2 )) dx we get 2μ = ∫_0 ^( 5) ((x^2 +(5−x)^2 )/((5−x)^2 +x^2 )) dx = ∫_0 ^( 5) dx 2μ = (x)_0 ^5 ⇒μ=(5/2)](Q124431.png)
$$\mu\:=\underset{\mathrm{0}} {\overset{\:\mathrm{5}} {\int}}\:\frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\left(\mathrm{5}−{x}\right)^{\mathrm{2}} }\:{dx}\:.\:\left[{use}\:{the}\:{interval}\:\right. \\ $$$$\left.{inverting}\:{substitution}\:{replacing}\:{x}\:{by}\:\mathrm{5}−{x}\:\right] \\ $$$$\mu\:\:=\underset{\mathrm{5}} {\overset{\:\mathrm{0}} {\int}}\:\frac{\left(\mathrm{5}−{x}\right)^{\mathrm{2}} }{\left(\mathrm{5}−{x}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} }\:\left(−{dx}\right)=\underset{\mathrm{0}} {\overset{\:\mathrm{5}} {\int}}\:\frac{\left(\mathrm{5}−{x}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} +\left(\mathrm{5}−{x}\right)^{\mathrm{2}} }\:{dx} \\ $$$${we}\:{get}\:\mathrm{2}\mu\:=\:\underset{\mathrm{0}} {\overset{\:\mathrm{5}} {\int}}\:\frac{{x}^{\mathrm{2}} +\left(\mathrm{5}−{x}\right)^{\mathrm{2}} }{\left(\mathrm{5}−{x}\right)^{\mathrm{2}} +{x}^{\mathrm{2}} }\:{dx}\:=\:\underset{\mathrm{0}} {\overset{\:\mathrm{5}} {\int}}\:{dx} \\ $$$$\mathrm{2}\mu\:=\:\left({x}\right)_{\mathrm{0}} ^{\mathrm{5}} \:\Rightarrow\mu=\frac{\mathrm{5}}{\mathrm{2}} \\ $$
