
Previous in Permutation and Combination Next in Permutation and Combination
Question Number 124400 by mr W last updated on 03/Dec/20

$${How}\:{many}\:{six}-{digit}\:{numbers}\:{contain} \\ $$$${exactly}\:{three}\:{different}\:{digits}? \\ $$
Answered by benjo_mathlover last updated on 03/Dec/20
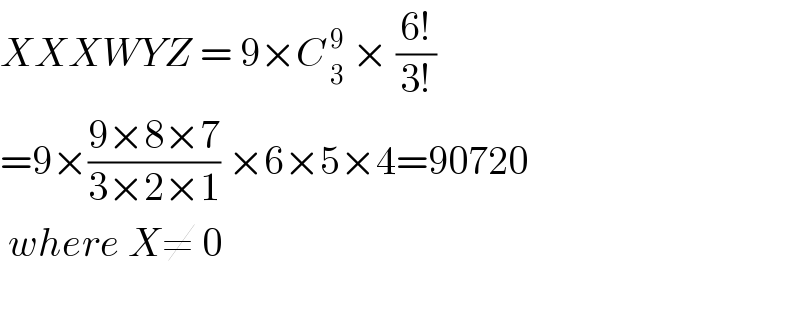
$${XXXWYZ}\:=\:\mathrm{9}×{C}_{\:\mathrm{3}} ^{\:\mathrm{9}} \:×\:\frac{\mathrm{6}!}{\mathrm{3}!} \\ $$$$=\mathrm{9}×\frac{\mathrm{9}×\mathrm{8}×\mathrm{7}}{\mathrm{3}×\mathrm{2}×\mathrm{1}}\:×\mathrm{6}×\mathrm{5}×\mathrm{4}=\mathrm{90720} \\ $$$$\:{where}\:{X}\neq\:\mathrm{0} \\ $$$$ \\ $$
Commented by benjo_mathlover last updated on 03/Dec/20
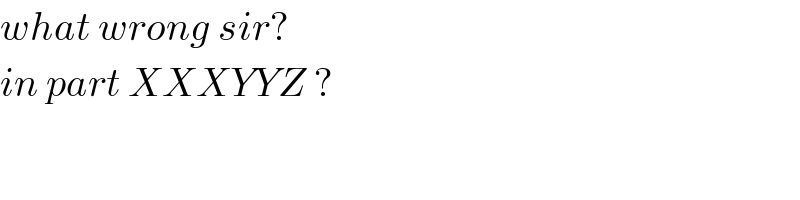
$${what}\:{wrong}\:{sir}?\: \\ $$$${in}\:{part}\:{XXXYYZ}\:? \\ $$
Answered by mr W last updated on 03/Dec/20

$${to}\:{select}\:{three}\:{digits}\:{there}\:{are}\: \\ $$$${C}_{\mathrm{3}} ^{\mathrm{10}} =\mathrm{120}\:{ways}. \\ $$$${say}\:{the}\:{three}\:{digits}\:{are}\:{x},{y},{z}. \\ $$$${to}\:{form}\:{a}\:\mathrm{6}\:{digit}\:{number}\:{with}\:{these} \\ $$$${three}\:{digits}\:{we}\:{have} \\ $$$${case}\:\mathrm{1}:\:\mathrm{4}{x}+{y}+{z} \\ $$$$\Rightarrow\mathrm{3}×\frac{\mathrm{6}!}{\mathrm{4}!}=\mathrm{90} \\ $$$${case}\:\mathrm{2}:\:\mathrm{3}{x}+\mathrm{2}{y}+{z} \\ $$$$\Rightarrow\mathrm{3}×\mathrm{2}×\frac{\mathrm{6}!}{\mathrm{3}!\mathrm{2}!}=\mathrm{360} \\ $$$${case}\:\mathrm{3}:\:\mathrm{2}{x}+\mathrm{2}{y}+\mathrm{2}{z} \\ $$$$\Rightarrow\frac{\mathrm{6}!}{\mathrm{2}!\mathrm{2}!\mathrm{2}!}=\mathrm{90} \\ $$$$\Rightarrow\mathrm{120}×\left(\mathrm{90}+\mathrm{360}+\mathrm{90}\right)=\mathrm{64800} \\ $$$$ \\ $$$${but}\:{in}\:{these}\:{numbers}\:{some}\:{begin} \\ $$$${with}\:{zero}: \\ $$$$\mathrm{0}{xxxxy}\:\Rightarrow\mathrm{2}×\frac{\mathrm{5}!}{\mathrm{4}!}=\mathrm{10} \\ $$$$\mathrm{0}{xxxyy}\:\Rightarrow\mathrm{2}×\frac{\mathrm{5}!}{\mathrm{3}!\mathrm{2}!}=\mathrm{20} \\ $$$$\mathrm{0}{xxxy}\mathrm{0}\:\Rightarrow\mathrm{2}×\frac{\mathrm{5}!}{\mathrm{3}!}=\mathrm{40} \\ $$$$\mathrm{0}{xxyy}\mathrm{0}\:\Rightarrow\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!}=\mathrm{30} \\ $$$$\mathrm{0}{xxy}\mathrm{00}\:\Rightarrow\mathrm{2}×\frac{\mathrm{5}!}{\mathrm{2}!\mathrm{2}!}=\mathrm{60} \\ $$$$\mathrm{0}{xy}\mathrm{000}\:\Rightarrow\frac{\mathrm{5}!}{\mathrm{3}!}=\mathrm{20} \\ $$$${to}\:{select}\:{the}\:{two}\:{digits}\:{x}\:{and}\:{y} \\ $$$${there}\:{are}\:{C}_{\mathrm{2}} ^{\mathrm{9}} =\mathrm{36}\:{ways}. \\ $$$$\Rightarrow\mathrm{36}×\left(\mathrm{10}+\mathrm{20}+\mathrm{40}+\mathrm{30}+\mathrm{60}+\mathrm{20}\right)=\mathrm{6480} \\ $$$$ \\ $$$${total}\:{valid}\:\mathrm{6}\:{digit}\:{numbers}: \\ $$$$\mathrm{64800}−\mathrm{6480}=\mathrm{58320} \\ $$
Commented by mr W last updated on 04/Dec/20
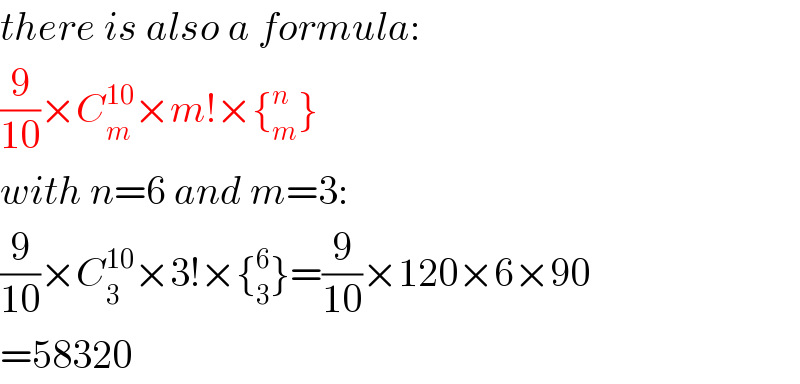
$${there}\:{is}\:{also}\:{a}\:{formula}: \\ $$$$\frac{\mathrm{9}}{\mathrm{10}}×{C}_{{m}} ^{\mathrm{10}} ×{m}!×\left\{_{{m}} ^{{n}} \right\} \\ $$$${with}\:{n}=\mathrm{6}\:{and}\:{m}=\mathrm{3}: \\ $$$$\frac{\mathrm{9}}{\mathrm{10}}×{C}_{\mathrm{3}} ^{\mathrm{10}} ×\mathrm{3}!×\left\{_{\mathrm{3}} ^{\mathrm{6}} \right\}=\frac{\mathrm{9}}{\mathrm{10}}×\mathrm{120}×\mathrm{6}×\mathrm{90} \\ $$$$=\mathrm{58320} \\ $$
