Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 124065 by Bird last updated on 30/Nov/20

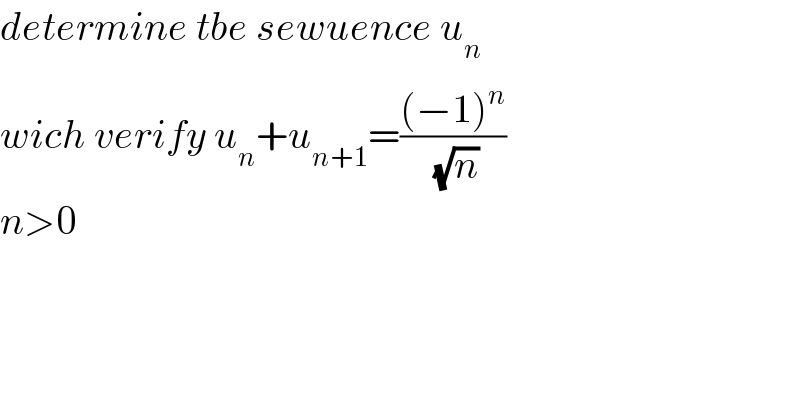
determine tbe sewuence u_n wich verify u_n +u_(n+1) =(((−1)^n )/( (√n))) n>0

$${determine}\:{tbe}\:{sewuence}\:{u}_{{n}} \\ $$ $${wich}\:{verify}\:{u}_{{n}} +{u}_{{n}+\mathrm{1}} =\frac{\left(−\mathrm{1}\right)^{{n}} }{\:\sqrt{{n}}} \\ $$ $${n}>\mathrm{0} \\ $$

Answered by mindispower last updated on 30/Nov/20

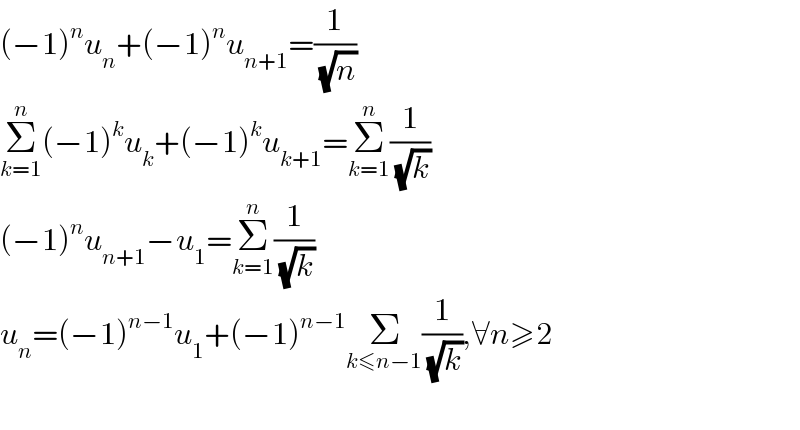
(−1)^n u_n +(−1)^n u_(n+1) =(1/( (√n))) Σ_(k=1) ^n (−1)^k u_k +(−1)^k u_(k+1) =Σ_(k=1) ^n (1/( (√k))) (−1)^n u_(n+1) −u_1 =Σ_(k=1) ^n (1/( (√k))) u_n =(−1)^(n−1) u_1 +(−1)^(n−1) Σ_(k≤n−1) (1/( (√k))),∀n≥2

$$\left(−\mathrm{1}\right)^{{n}} {u}_{{n}} +\left(−\mathrm{1}\right)^{{n}} {u}_{{n}+\mathrm{1}} =\frac{\mathrm{1}}{\:\sqrt{{n}}} \\ $$ $$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left(−\mathrm{1}\right)^{{k}} {u}_{{k}} +\left(−\mathrm{1}\right)^{{k}} {u}_{{k}+\mathrm{1}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{k}}} \\ $$ $$\left(−\mathrm{1}\right)^{{n}} {u}_{{n}+\mathrm{1}} −{u}_{\mathrm{1}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{k}}} \\ $$ $${u}_{{n}} =\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {u}_{\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \underset{{k}\leqslant{n}−\mathrm{1}} {\sum}\frac{\mathrm{1}}{\:\sqrt{{k}}},\forall{n}\geqslant\mathrm{2} \\ $$ $$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com