
Question Number 124001 by Don08q last updated on 30/Nov/20

$$\mathrm{A}\:\mathrm{variable}\:\mathrm{point}\:{P}\left({x},\:{y}\right)\:\mathrm{moves}\:\mathrm{on}\:\mathrm{the} \\ $$$$\mathrm{curve}\:\:{xy}\:=\:\mathrm{6}\:\mathrm{and}\:{R}\:\mathrm{is}\:\mathrm{the}\:\mathrm{point}\:\mathrm{which}\: \\ $$$$\mathrm{divides}\:\mathrm{the}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{that}\:\mathrm{joins}\:\mathrm{the} \\ $$$$\mathrm{points}\:{A}\left(−\mathrm{2},\:\mathrm{0}\right)\:\:\mathrm{and}\:\:{B}\left(\mathrm{0},\:−\mathrm{1}\right)\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{ratio}\:\mathrm{3}:\mathrm{1},\:\mathrm{internally}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{locus}\:\mathrm{of} \\ $$$${PR}. \\ $$
Answered by liberty last updated on 30/Nov/20
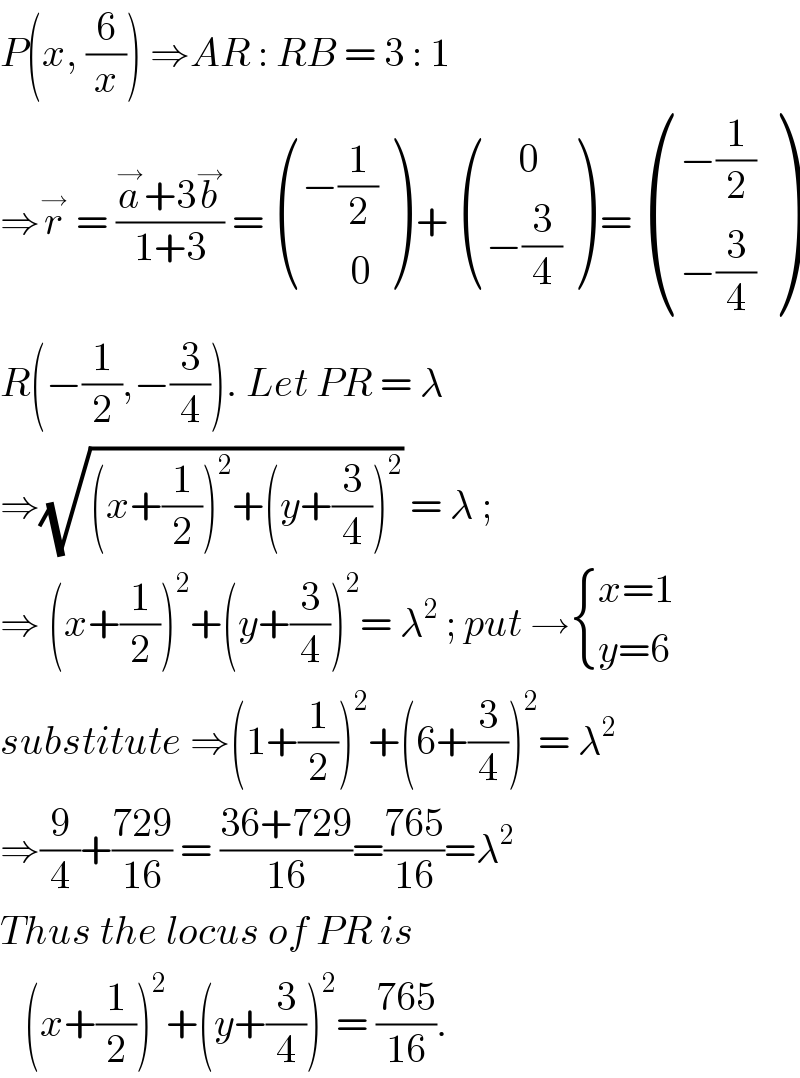
$${P}\left({x},\:\frac{\mathrm{6}}{{x}}\right)\:\Rightarrow{AR}\::\:{RB}\:=\:\mathrm{3}\::\:\mathrm{1} \\ $$$$\Rightarrow\overset{\rightarrow} {{r}}\:=\:\frac{\overset{\rightarrow} {{a}}+\mathrm{3}\overset{\rightarrow} {{b}}}{\mathrm{1}+\mathrm{3}}\:=\:\begin{pmatrix}{−\frac{\mathrm{1}}{\mathrm{2}}}\\{\:\:\:\:\:\:\mathrm{0}}\end{pmatrix}\:+\:\begin{pmatrix}{\:\:\:\:\mathrm{0}}\\{−\frac{\mathrm{3}}{\mathrm{4}}}\end{pmatrix}\:=\:\begin{pmatrix}{−\frac{\mathrm{1}}{\mathrm{2}}}\\{−\frac{\mathrm{3}}{\mathrm{4}}}\end{pmatrix} \\ $$$${R}\left(−\frac{\mathrm{1}}{\mathrm{2}},−\frac{\mathrm{3}}{\mathrm{4}}\right).\:{Let}\:{PR}\:=\:\lambda\: \\ $$$$\Rightarrow\sqrt{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} }\:=\:\lambda\:;\: \\ $$$$\Rightarrow\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} =\:\lambda^{\mathrm{2}} \:;\:{put}\:\rightarrow\begin{cases}{{x}=\mathrm{1}}\\{{y}=\mathrm{6}}\end{cases} \\ $$$${substitute}\:\Rightarrow\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\mathrm{6}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} =\:\lambda^{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{729}}{\mathrm{16}}\:=\:\frac{\mathrm{36}+\mathrm{729}}{\mathrm{16}}=\frac{\mathrm{765}}{\mathrm{16}}=\lambda^{\mathrm{2}} \\ $$$${Thus}\:{the}\:{locus}\:{of}\:{PR}\:{is}\: \\ $$$$\:\:\:\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left({y}+\frac{\mathrm{3}}{\mathrm{4}}\right)^{\mathrm{2}} =\:\frac{\mathrm{765}}{\mathrm{16}}.\: \\ $$
Commented by Don08q last updated on 30/Nov/20
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{Sir}. \\ $$
