
Question Number 123996 by mlj5 last updated on 29/Nov/20
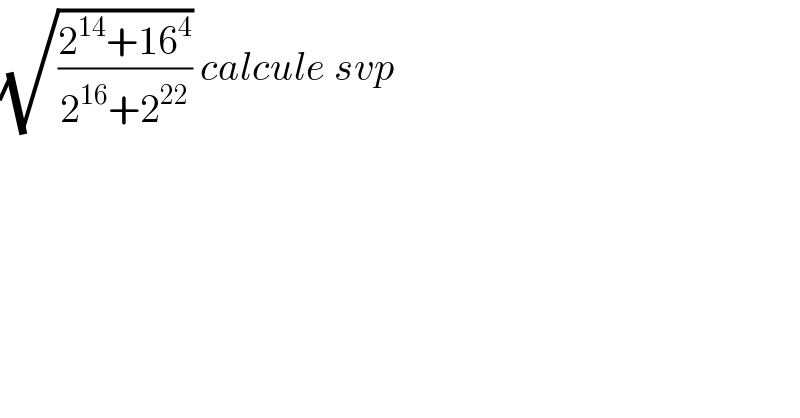
$$\sqrt{\frac{\mathrm{2}^{\mathrm{14}} +\mathrm{16}^{\mathrm{4}} }{\mathrm{2}^{\mathrm{16}} +\mathrm{2}^{\mathrm{22}} }}\:{calcule}\:{svp} \\ $$
Answered by john_santu last updated on 30/Nov/20
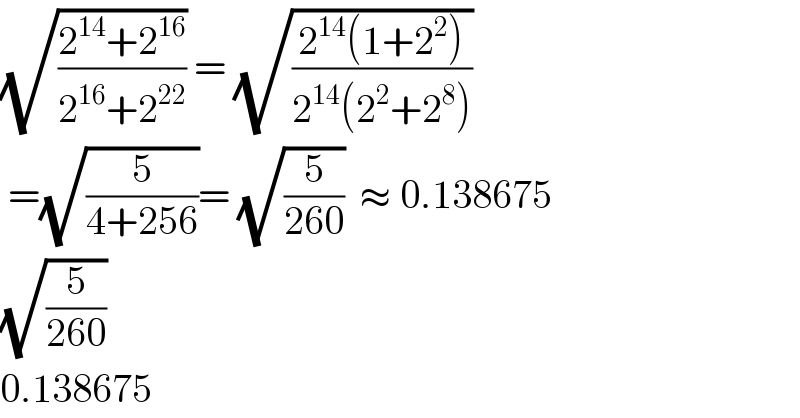
$$\sqrt{\frac{\mathrm{2}^{\mathrm{14}} +\mathrm{2}^{\mathrm{16}} }{\mathrm{2}^{\mathrm{16}} +\mathrm{2}^{\mathrm{22}} }}\:=\:\sqrt{\frac{\mathrm{2}^{\mathrm{14}} \left(\mathrm{1}+\mathrm{2}^{\mathrm{2}} \right)}{\mathrm{2}^{\mathrm{14}} \left(\mathrm{2}^{\mathrm{2}} +\mathrm{2}^{\mathrm{8}} \right)}} \\ $$$$\:=\sqrt{\frac{\mathrm{5}}{\mathrm{4}+\mathrm{256}}}=\:\sqrt{\frac{\mathrm{5}}{\mathrm{260}}}\:\:\approx\:\mathrm{0}.\mathrm{138675} \\ $$$$\sqrt{\frac{\mathrm{5}}{\mathrm{260}}} \\ $$$$\mathrm{0}.\mathrm{138675} \\ $$
