
Previous in Matrices and Determinants Next in Matrices and Determinants
Question Number 123868 by benjo_mathlover last updated on 28/Nov/20

Answered by liberty last updated on 29/Nov/20
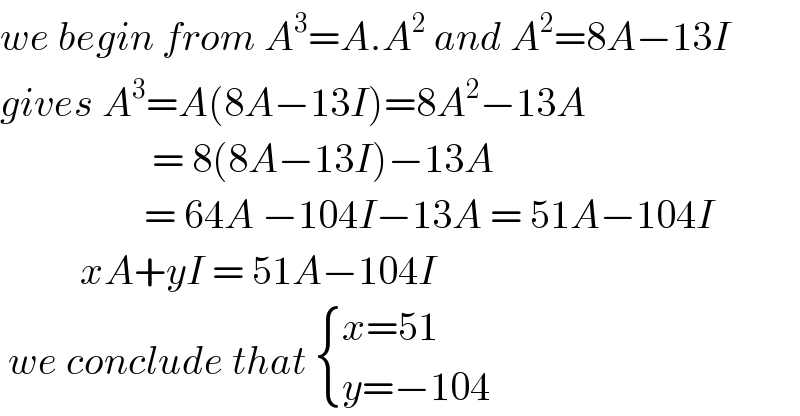
$${we}\:{begin}\:{from}\:{A}^{\mathrm{3}} ={A}.{A}^{\mathrm{2}} \:{and}\:{A}^{\mathrm{2}} =\mathrm{8}{A}−\mathrm{13}{I} \\ $$$${gives}\:{A}^{\mathrm{3}} ={A}\left(\mathrm{8}{A}−\mathrm{13}{I}\right)=\mathrm{8}{A}^{\mathrm{2}} −\mathrm{13}{A} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{8}\left(\mathrm{8}{A}−\mathrm{13}{I}\right)−\mathrm{13}{A}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{64}{A}\:−\mathrm{104}{I}−\mathrm{13}{A}\:=\:\mathrm{51}{A}−\mathrm{104}{I} \\ $$$$\:\:\:\:\:\:\:\:\:\:{xA}+{yI}\:=\:\mathrm{51}{A}−\mathrm{104}{I}\: \\ $$$$\:{we}\:{conclude}\:{that}\:\begin{cases}{{x}=\mathrm{51}}\\{{y}=−\mathrm{104}}\end{cases} \\ $$
