
Question Number 123777 by 676597498 last updated on 28/Nov/20

Commented by MJS_new last updated on 28/Nov/20
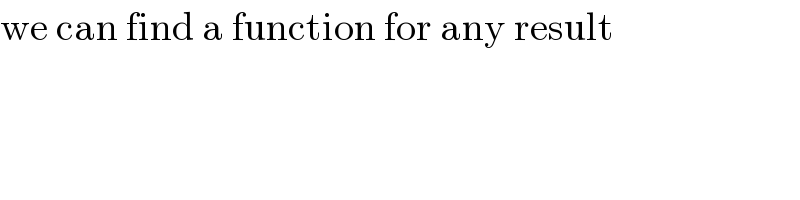
$$\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{a}\:\mathrm{function}\:\mathrm{for}\:\mathrm{any}\:\mathrm{result} \\ $$
Answered by Olaf last updated on 28/Nov/20

$${u}\left({n}\right)\:=\:{n}^{\mathrm{3}} −\mathrm{1} \\ $$$${u}\left(\mathrm{2}\right)\:=\:\mathrm{7} \\ $$$${u}\left(\mathrm{3}\right)\:=\:\mathrm{26} \\ $$$${u}\left(\mathrm{4}\right)\:=\:\mathrm{63} \\ $$$${u}\left(\mathrm{5}\right)\:=\:\mathrm{124} \\ $$$${u}\left(\mathrm{6}\right)\:=\:\mathrm{215} \\ $$$$\mathrm{OEIS}\:\mathrm{A068601} \\ $$$$\mathrm{http}://\mathrm{oeis}.\mathrm{org}/\mathrm{A068601} \\ $$
Commented by MJS_new last updated on 28/Nov/20

$$\mathrm{I}\:\mathrm{saw}\:\mathrm{this}\:\mathrm{solution}\:\mathrm{too}.\:\mathrm{but}\:\mathrm{as}\:\mathrm{you}\:\mathrm{know},\:\mathrm{we} \\ $$$$\mathrm{are}\:\mathrm{not}\:\mathrm{limited}\:\mathrm{to}\:\mathrm{polynomials}...\:\mathrm{I}'\mathrm{m}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{opinion},\:\mathrm{if}\:\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{know}\:\mathrm{what}\:\mathrm{we}\:\mathrm{are}\:\mathrm{allowed} \\ $$$$\mathrm{to}\:\mathrm{use},\:\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\mathrm{what}\:\mathrm{we}\:\mathrm{want}. \\ $$$${a}_{\mathrm{1}} =−\mathrm{12} \\ $$$${a}_{\mathrm{2}} =−\mathrm{11} \\ $$$${a}_{\mathrm{3}} =\mathrm{2} \\ $$$${a}_{\mathrm{4}} =\mathrm{28} \\ $$$${a}_{{n}} ={a}_{{n}−\mathrm{4}} +{a}_{{n}−\mathrm{3}} +{a}_{{n}−\mathrm{2}} +{a}_{{n}−\mathrm{1}} \forall{n}>\mathrm{4} \\ $$$${a}_{\mathrm{5}} =\mathrm{7} \\ $$$${a}_{\mathrm{6}} =\mathrm{26} \\ $$$${a}_{\mathrm{7}} =\mathrm{63} \\ $$$${a}_{\mathrm{8}} =\mathrm{124} \\ $$$${a}_{\mathrm{9}} =\mathrm{220} \\ $$
