
Question Number 123681 by ZiYangLee last updated on 27/Nov/20

$$\mathrm{How}\:\mathrm{many}\:\mathrm{3}-\mathrm{digits}\:\mathrm{positive}\:\mathrm{integers} \\ $$$$\mathrm{are}\:\mathrm{there}\:\mathrm{such}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{digits}\: \\ $$$$\mathrm{is}\:\mathrm{10}? \\ $$
Answered by mr W last updated on 27/Nov/20
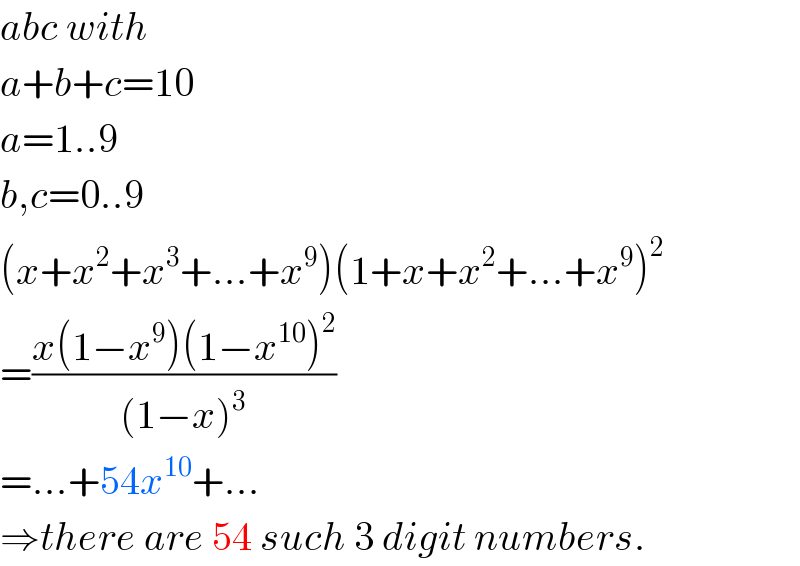
$${abc}\:{with} \\ $$$${a}+{b}+{c}=\mathrm{10} \\ $$$${a}=\mathrm{1}..\mathrm{9} \\ $$$${b},{c}=\mathrm{0}..\mathrm{9} \\ $$$$\left({x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +...+{x}^{\mathrm{9}} \right)\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +...+{x}^{\mathrm{9}} \right)^{\mathrm{2}} \\ $$$$=\frac{{x}\left(\mathrm{1}−{x}^{\mathrm{9}} \right)\left(\mathrm{1}−{x}^{\mathrm{10}} \right)^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$$=...+\mathrm{54}{x}^{\mathrm{10}} +... \\ $$$$\Rightarrow{there}\:{are}\:\mathrm{54}\:{such}\:\mathrm{3}\:{digit}\:{numbers}. \\ $$
Commented by malwan last updated on 27/Nov/20
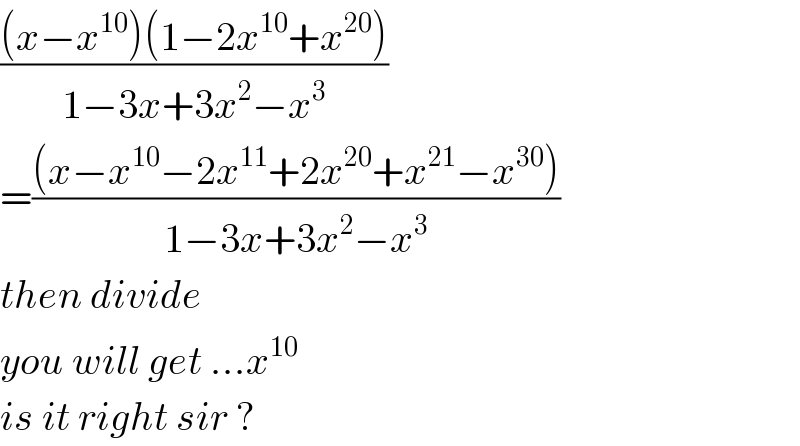
$$\frac{\left({x}−{x}^{\mathrm{10}} \right)\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{10}} +{x}^{\mathrm{20}} \right)}{\mathrm{1}−\mathrm{3}{x}+\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{3}} } \\ $$$$=\frac{\left({x}−{x}^{\mathrm{10}} −\mathrm{2}{x}^{\mathrm{11}} +\mathrm{2}{x}^{\mathrm{20}} +{x}^{\mathrm{21}} −{x}^{\mathrm{30}} \right)}{\mathrm{1}−\mathrm{3}{x}+\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{3}} } \\ $$$${then}\:{divide}\: \\ $$$${you}\:{will}\:{get}\:...{x}^{\mathrm{10}} \\ $$$${is}\:{it}\:{right}\:{sir}\:? \\ $$
Commented by mr W last updated on 27/Nov/20
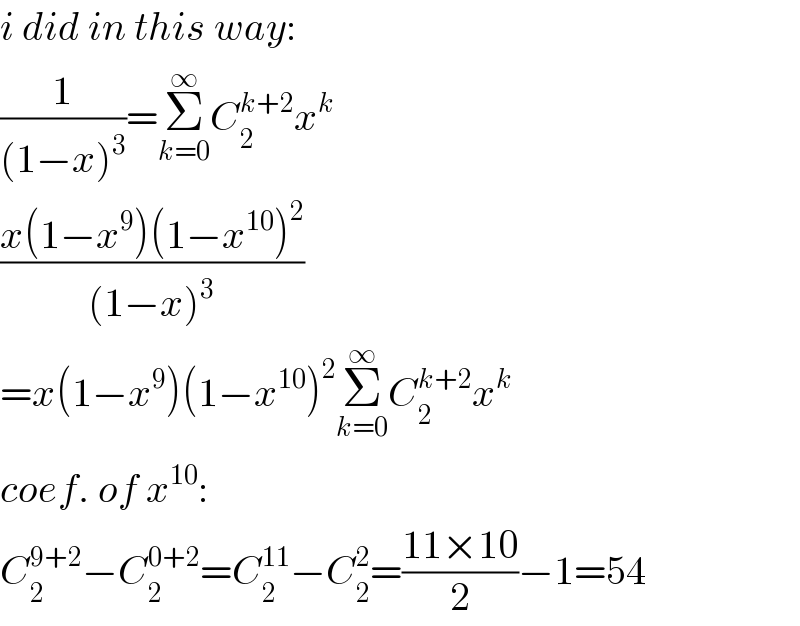
$${i}\:{did}\:{in}\:{this}\:{way}: \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{2}} ^{{k}+\mathrm{2}} {x}^{{k}} \\ $$$$\frac{{x}\left(\mathrm{1}−{x}^{\mathrm{9}} \right)\left(\mathrm{1}−{x}^{\mathrm{10}} \right)^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$$={x}\left(\mathrm{1}−{x}^{\mathrm{9}} \right)\left(\mathrm{1}−{x}^{\mathrm{10}} \right)^{\mathrm{2}} \underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{C}_{\mathrm{2}} ^{{k}+\mathrm{2}} {x}^{{k}} \\ $$$${coef}.\:{of}\:{x}^{\mathrm{10}} : \\ $$$${C}_{\mathrm{2}} ^{\mathrm{9}+\mathrm{2}} −{C}_{\mathrm{2}} ^{\mathrm{0}+\mathrm{2}} ={C}_{\mathrm{2}} ^{\mathrm{11}} −{C}_{\mathrm{2}} ^{\mathrm{2}} =\frac{\mathrm{11}×\mathrm{10}}{\mathrm{2}}−\mathrm{1}=\mathrm{54} \\ $$
Commented by malwan last updated on 28/Nov/20

$${fantastic}\:{sir} \\ $$$${thank}\:{you} \\ $$
Answered by floor(10²Eta[1]) last updated on 27/Nov/20

$$\mathrm{109} \\ $$$$\mathrm{118} \\ $$$$\mathrm{127} \\ $$$$\mathrm{136} \\ $$$$\mathrm{145} \\ $$$$\mathrm{154} \\ $$$$\mathrm{163} \\ $$$$\mathrm{172} \\ $$$$\mathrm{181} \\ $$$$\mathrm{190} \\ $$$$\left(\mathrm{10}\:\mathrm{cases}\right) \\ $$$$\mathrm{208} \\ $$$$\mathrm{217} \\ $$$$\mathrm{226} \\ $$$$\mathrm{235} \\ $$$$\mathrm{244} \\ $$$$\mathrm{253} \\ $$$$\mathrm{262} \\ $$$$\mathrm{271} \\ $$$$\mathrm{280} \\ $$$$\left(\mathrm{9}\:\mathrm{cases}\right) \\ $$$$\mathrm{307} \\ $$$$\mathrm{316} \\ $$$$\mathrm{325} \\ $$$$\mathrm{334} \\ $$$$\mathrm{343} \\ $$$$\mathrm{352} \\ $$$$\mathrm{361} \\ $$$$\mathrm{370} \\ $$$$\left(\mathrm{8}\:\mathrm{cases}\right) \\ $$$$... \\ $$$$\mathrm{901} \\ $$$$\mathrm{910} \\ $$$$\left(\mathrm{2}\:\mathrm{cases}\right) \\ $$$$\mathrm{total}\:\mathrm{cases}:\:\mathrm{10}+\mathrm{9}+\mathrm{8}+...+\mathrm{2}=\mathrm{54} \\ $$
