
Question Number 123488 by peter frank last updated on 25/Nov/20
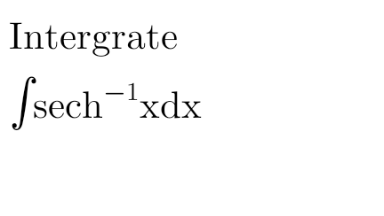
Answered by MJS_new last updated on 25/Nov/20
![x=sech y =(1/(cosh y))=((2e^y )/(e^(2y) +1)) ⇒ y=ln ((1+(√(1−x^2 )))/x) =sech^(−1) x ∫sech^(−1) x dx=∫ln ((1+(√(1−x^2 )))/x) dx= [by parts] =xln ((1+(√(1−x^2 )))/x) +∫(dx/( (√(1−x^2 ))))= =xln ((1+(√(1−x^2 )))/x) +arcsin x +C [=xsech^(−1) x +arcsin x +C]](Q123492.png)
$${x}=\mathrm{sech}\:{y}\:=\frac{\mathrm{1}}{\mathrm{cosh}\:{y}}=\frac{\mathrm{2e}^{{y}} }{\mathrm{e}^{\mathrm{2}{y}} +\mathrm{1}} \\ $$$$\Rightarrow\:{y}=\mathrm{ln}\:\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:=\mathrm{sech}^{−\mathrm{1}} \:{x} \\ $$$$\int\mathrm{sech}^{−\mathrm{1}} \:{x}\:{dx}=\int\mathrm{ln}\:\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:{dx}= \\ $$$$\:\:\:\:\:\left[\mathrm{by}\:\mathrm{parts}\right] \\ $$$$={x}\mathrm{ln}\:\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:+\int\frac{{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}= \\ $$$$={x}\mathrm{ln}\:\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:+\mathrm{arcsin}\:{x}\:+{C} \\ $$$$\left[={x}\mathrm{sech}^{−\mathrm{1}} \:{x}\:+\mathrm{arcsin}\:{x}\:+{C}\right] \\ $$
Answered by Dwaipayan Shikari last updated on 26/Nov/20
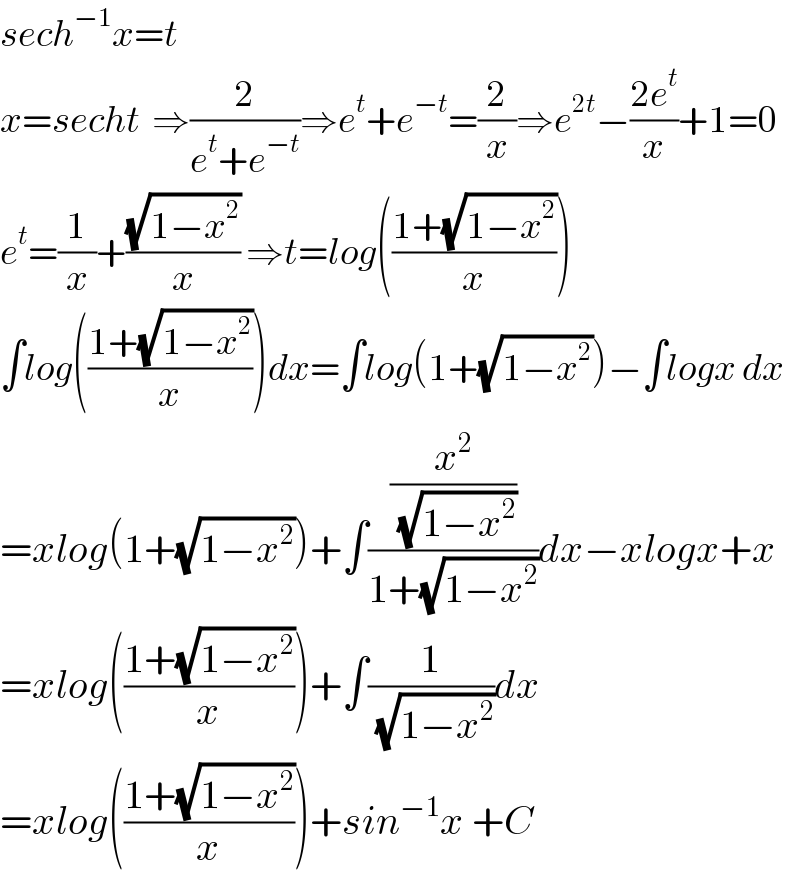
$${sech}^{−\mathrm{1}} {x}={t} \\ $$$${x}={secht}\:\:\Rightarrow\frac{\mathrm{2}}{{e}^{{t}} +{e}^{−{t}} }\Rightarrow{e}^{{t}} +{e}^{−{t}} =\frac{\mathrm{2}}{{x}}\Rightarrow{e}^{\mathrm{2}{t}} −\frac{\mathrm{2}{e}^{{t}} }{{x}}+\mathrm{1}=\mathrm{0} \\ $$$${e}^{{t}} =\frac{\mathrm{1}}{{x}}+\frac{\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\:\Rightarrow{t}={log}\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\right) \\ $$$$\int{log}\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\right){dx}=\int{log}\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)−\int{logx}\:{dx} \\ $$$$={xlog}\left(\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)+\int\frac{\frac{{x}^{\mathrm{2}} }{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}}{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}−{xlogx}+{x} \\ $$$$={xlog}\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\right)+\int\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}\: \\ $$$$={xlog}\left(\frac{\mathrm{1}+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{{x}}\right)+{sin}^{−\mathrm{1}} {x}\:+{C} \\ $$
Commented by peter frank last updated on 26/Nov/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
