
Question Number 123389 by aurpeyz last updated on 25/Nov/20
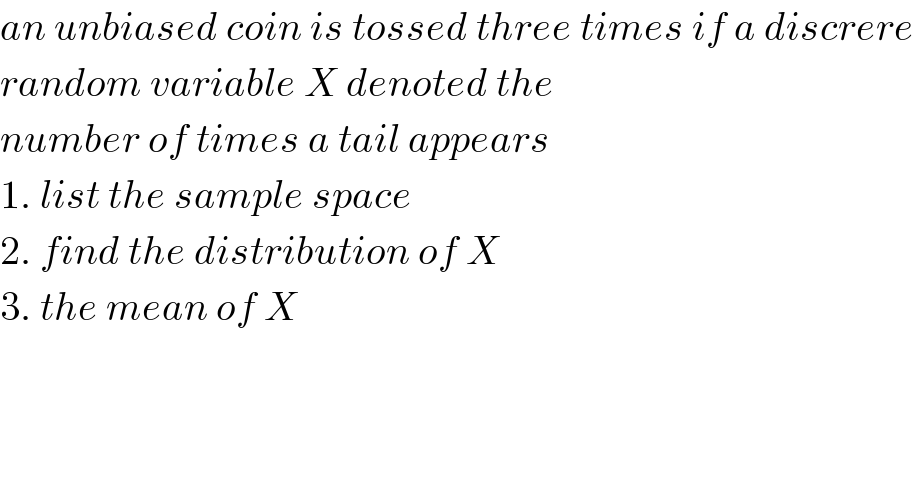
$${an}\:{unbiased}\:{coin}\:{is}\:{tossed}\:{three}\:{times}\:{if}\:{a}\:{discrere} \\ $$$${random}\:{variable}\:{X}\:{denoted}\:{the}\: \\ $$$${number}\:{of}\:{times}\:{a}\:{tail}\:{appears}\: \\ $$$$\mathrm{1}.\:{list}\:{the}\:{sample}\:{space} \\ $$$$\mathrm{2}.\:{find}\:{the}\:{distribution}\:{of}\:{X} \\ $$$$\mathrm{3}.\:{the}\:{mean}\:{of}\:{X} \\ $$
Answered by som(math1967) last updated on 25/Nov/20
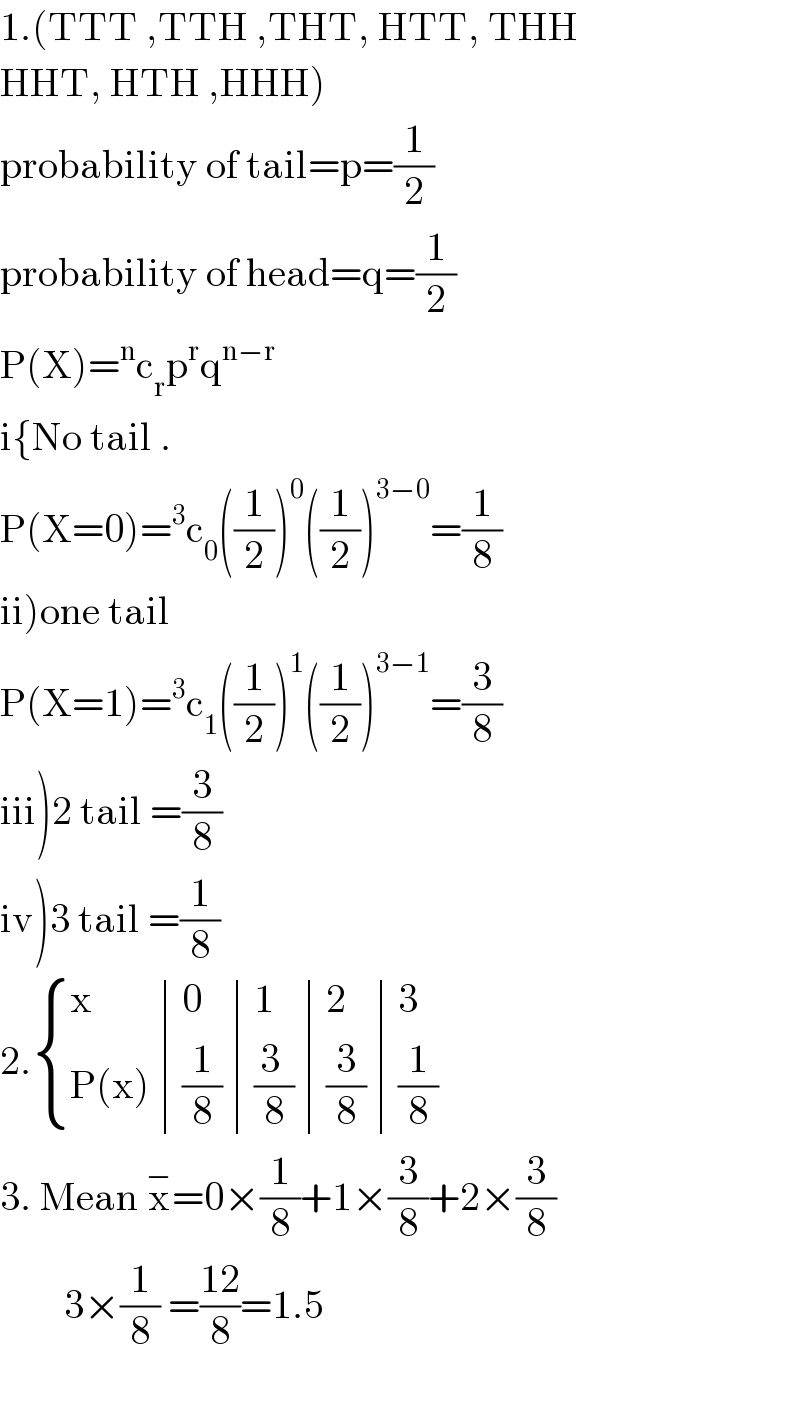
$$\mathrm{1}.\left(\mathrm{TTT}\:,\mathrm{TTH}\:,\mathrm{THT},\:\mathrm{HTT},\:\mathrm{THH}\right. \\ $$$$\left.\mathrm{HHT},\:\mathrm{HTH}\:,\mathrm{HHH}\right) \\ $$$$\mathrm{probability}\:\mathrm{of}\:\mathrm{tail}=\mathrm{p}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{probability}\:\mathrm{of}\:\mathrm{head}=\mathrm{q}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{P}\left(\mathrm{X}\right)=^{\mathrm{n}} \mathrm{c}_{\mathrm{r}} \mathrm{p}^{\mathrm{r}} \mathrm{q}^{\mathrm{n}−\mathrm{r}} \\ $$$$\mathrm{i}\left\{\mathrm{No}\:\mathrm{tail}\:.\right. \\ $$$$\mathrm{P}\left(\mathrm{X}=\mathrm{0}\right)=^{\mathrm{3}} \mathrm{c}_{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{0}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}−\mathrm{0}} =\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\left.\mathrm{ii}\right)\mathrm{one}\:\mathrm{tail} \\ $$$$\mathrm{P}\left(\mathrm{X}=\mathrm{1}\right)=^{\mathrm{3}} \mathrm{c}_{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}−\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\left.\mathrm{iii}\right)\mathrm{2}\:\mathrm{tail}\:=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\left.\mathrm{iv}\right)\mathrm{3}\:\mathrm{tail}\:=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$$\mathrm{2}.\begin{cases}{\mathrm{x}}&{\mathrm{0}}&{\mathrm{1}}&{\mathrm{2}}&{\mathrm{3}}\\{\mathrm{P}\left(\mathrm{x}\right)}&{\frac{\mathrm{1}}{\mathrm{8}}}&{\frac{\mathrm{3}\:}{\mathrm{8}}}&{\frac{\mathrm{3}}{\mathrm{8}}}&{\frac{\mathrm{1}}{\mathrm{8}}}\end{cases}\: \\ $$$$\mathrm{3}.\:\mathrm{Mean}\:\overset{−} {\mathrm{x}}=\mathrm{0}×\frac{\mathrm{1}}{\mathrm{8}}+\mathrm{1}×\frac{\mathrm{3}}{\mathrm{8}}+\mathrm{2}×\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\:\:\:\:\:\:\:\:\mathrm{3}×\frac{\mathrm{1}}{\mathrm{8}}\:=\frac{\mathrm{12}}{\mathrm{8}}=\mathrm{1}.\mathrm{5} \\ $$$$ \\ $$
