
Question Number 123294 by roniee last updated on 24/Nov/20
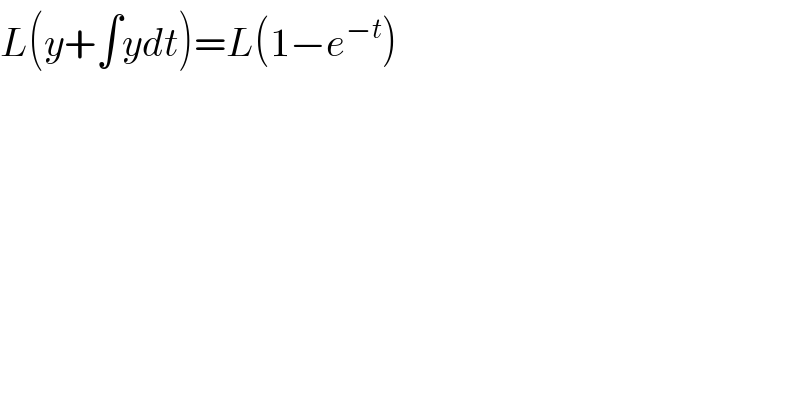
$${L}\left({y}+\int{ydt}\right)={L}\left(\mathrm{1}−{e}^{−{t}} \right) \\ $$
Answered by Olaf last updated on 24/Nov/20
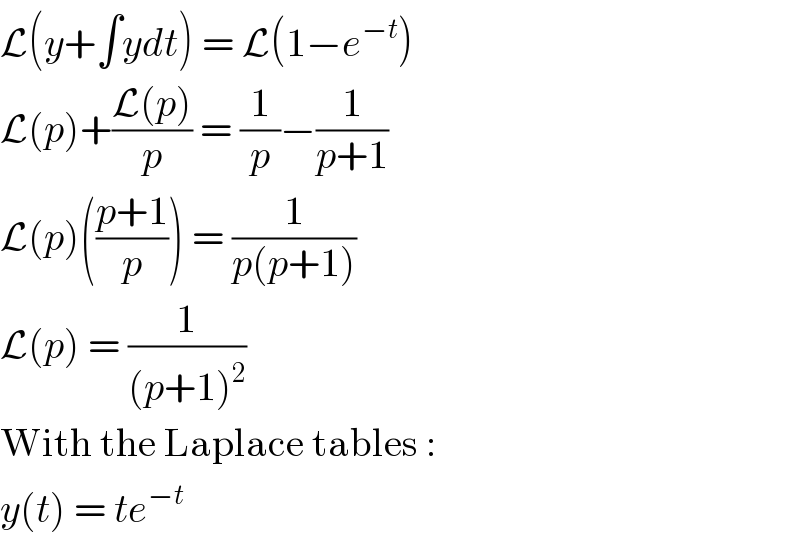
$$\mathcal{L}\left({y}+\int{ydt}\right)\:=\:\mathcal{L}\left(\mathrm{1}−{e}^{−{t}} \right) \\ $$$$\mathcal{L}\left({p}\right)+\frac{\mathcal{L}\left({p}\right)}{{p}}\:=\:\frac{\mathrm{1}}{{p}}−\frac{\mathrm{1}}{{p}+\mathrm{1}} \\ $$$$\mathcal{L}\left({p}\right)\left(\frac{{p}+\mathrm{1}}{{p}}\right)\:=\:\frac{\mathrm{1}}{{p}\left({p}+\mathrm{1}\right)} \\ $$$$\mathcal{L}\left({p}\right)\:=\:\frac{\mathrm{1}}{\left({p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{With}\:\mathrm{the}\:\mathrm{Laplace}\:\mathrm{tables}\:: \\ $$$${y}\left({t}\right)\:=\:{te}^{−{t}} \\ $$
