
Question Number 122938 by CanovasCamiseros last updated on 21/Nov/20

Commented by CanovasCamiseros last updated on 21/Nov/20

$$\boldsymbol{{help}} \\ $$
Answered by Dwaipayan Shikari last updated on 21/Nov/20
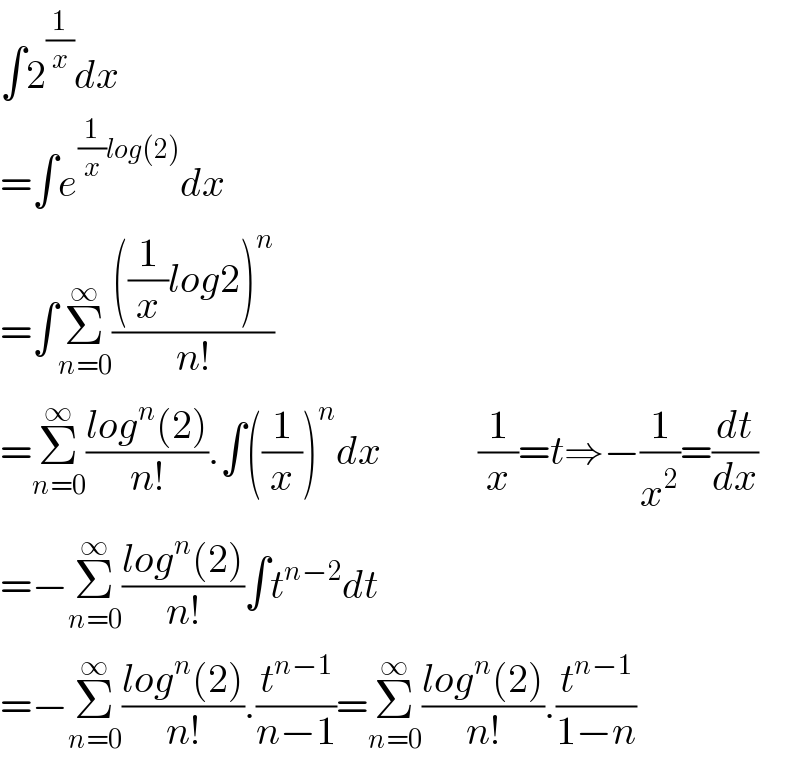
$$\int\mathrm{2}^{\frac{\mathrm{1}}{{x}}} {dx} \\ $$$$=\int{e}^{\frac{\mathrm{1}}{{x}}{log}\left(\mathrm{2}\right)} {dx} \\ $$$$=\int\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(\frac{\mathrm{1}}{{x}}{log}\mathrm{2}\right)^{{n}} }{{n}!} \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{log}^{{n}} \left(\mathrm{2}\right)}{{n}!}.\int\left(\frac{\mathrm{1}}{{x}}\right)^{{n}} {dx}\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{{x}}={t}\Rightarrow−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\frac{{dt}}{{dx}} \\ $$$$=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{log}^{{n}} \left(\mathrm{2}\right)}{{n}!}\int{t}^{{n}−\mathrm{2}} {dt} \\ $$$$=−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{log}^{{n}} \left(\mathrm{2}\right)}{{n}!}.\frac{{t}^{{n}−\mathrm{1}} }{{n}−\mathrm{1}}=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{log}^{{n}} \left(\mathrm{2}\right)}{{n}!}.\frac{{t}^{{n}−\mathrm{1}} }{\mathrm{1}−{n}} \\ $$
