
Question Number 122922 by bemath last updated on 21/Nov/20
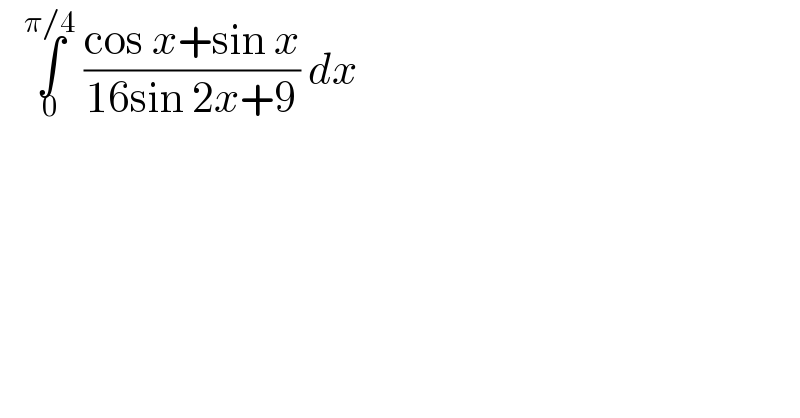
$$\:\:\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\frac{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\mathrm{16sin}\:\mathrm{2}{x}+\mathrm{9}}\:{dx}\: \\ $$
Answered by liberty last updated on 21/Nov/20
![ς = ∫_0 ^(π/4) ((cos x+sin x)/(16sin 2x+9)) dx [ let 16sin 2x+9 = t ⇒dt=32cos 2x dx ] ⇒dt = 32 (cos x+sin x)(cos x−sin x)dx ⇒dt=32(cos x+sin x)(√(1−sin 2x)) dx ⇒dt=32(cos x+sin x)(√(1−(((t−9)/(16))))) dx ⇒(cos x+sin x)dx = (dt/(32 (√((25−t)/(16)))))=(dt/(8(√(25−t)))) ς = ∫_9 ^(25) (dt/(8t(√(25−t)))) =(1/( 8))∫_9 ^(25) (dt/(t(√(25−t)))) [ let (√(25−t)) = s ⇒t=25−s^2 ] ς = (1/8)∫_4 ^0 ((−2s ds)/(s(25−s^2 )))= (1/4)∫_0 ^4 (ds/(25−s^2 )) [ ((−1)/((s+5)(s−5))) = (A/(s+5)) + (B/(s−5)) ] [ A=((−1)/(s−5))∣_(s=−5) = (1/(10)) ∧ B = ((−1)/(s+5)) ∣_(s=5) =−(1/(10)) ] ς = (1/(40)) (∫_0 ^4 (ds/(s+5))−∫_0 ^4 (ds/(s−5))) ς = (1/(40)) (ln ∣((s+5)/(s−5))∣)_0 ^4 = ((ln (9))/(40)).▲](Q122924.png)
$$\varsigma\:=\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\frac{\mathrm{cos}\:{x}+\mathrm{sin}\:{x}}{\mathrm{16sin}\:\mathrm{2}{x}+\mathrm{9}}\:{dx}\: \\ $$$$\:\left[\:{let}\:\mathrm{16sin}\:\mathrm{2}{x}+\mathrm{9}\:=\:{t}\:\Rightarrow{dt}=\mathrm{32cos}\:\mathrm{2}{x}\:{dx}\:\right] \\ $$$$\:\Rightarrow{dt}\:=\:\mathrm{32}\:\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)\left(\mathrm{cos}\:{x}−\mathrm{sin}\:{x}\right){dx} \\ $$$$\Rightarrow{dt}=\mathrm{32}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)\sqrt{\mathrm{1}−\mathrm{sin}\:\mathrm{2}{x}}\:{dx} \\ $$$$\Rightarrow{dt}=\mathrm{32}\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right)\sqrt{\mathrm{1}−\left(\frac{{t}−\mathrm{9}}{\mathrm{16}}\right)}\:{dx} \\ $$$$\Rightarrow\left(\mathrm{cos}\:{x}+\mathrm{sin}\:{x}\right){dx}\:=\:\frac{{dt}}{\mathrm{32}\:\sqrt{\frac{\mathrm{25}−{t}}{\mathrm{16}}}}=\frac{{dt}}{\mathrm{8}\sqrt{\mathrm{25}−{t}}} \\ $$$$\varsigma\:=\:\int_{\mathrm{9}} ^{\mathrm{25}} \frac{{dt}}{\mathrm{8}{t}\sqrt{\mathrm{25}−{t}}}\:=\frac{\mathrm{1}}{\:\mathrm{8}}\int_{\mathrm{9}} ^{\mathrm{25}} \frac{{dt}}{{t}\sqrt{\mathrm{25}−{t}}} \\ $$$$\:\left[\:{let}\:\sqrt{\mathrm{25}−{t}}\:=\:{s}\:\Rightarrow{t}=\mathrm{25}−{s}^{\mathrm{2}} \:\right]\: \\ $$$$\varsigma\:=\:\frac{\mathrm{1}}{\mathrm{8}}\int_{\mathrm{4}} ^{\mathrm{0}} \frac{−\mathrm{2}{s}\:{ds}}{{s}\left(\mathrm{25}−{s}^{\mathrm{2}} \right)}=\:\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\mathrm{4}} \frac{{ds}}{\mathrm{25}−{s}^{\mathrm{2}} } \\ $$$$\left[\:\frac{−\mathrm{1}}{\left({s}+\mathrm{5}\right)\left({s}−\mathrm{5}\right)}\:=\:\frac{{A}}{{s}+\mathrm{5}}\:+\:\frac{{B}}{{s}−\mathrm{5}}\:\right] \\ $$$$\:\left[\:{A}=\frac{−\mathrm{1}}{{s}−\mathrm{5}}\mid_{{s}=−\mathrm{5}} \:=\:\frac{\mathrm{1}}{\mathrm{10}}\:\wedge\:{B}\:=\:\frac{−\mathrm{1}}{{s}+\mathrm{5}}\:\mid_{{s}=\mathrm{5}} =−\frac{\mathrm{1}}{\mathrm{10}}\:\right] \\ $$$$\varsigma\:=\:\frac{\mathrm{1}}{\mathrm{40}}\:\left(\int_{\mathrm{0}} ^{\mathrm{4}} \frac{{ds}}{{s}+\mathrm{5}}−\int_{\mathrm{0}} ^{\mathrm{4}} \frac{{ds}}{{s}−\mathrm{5}}\right) \\ $$$$\varsigma\:=\:\frac{\mathrm{1}}{\mathrm{40}}\:\left(\mathrm{ln}\:\mid\frac{{s}+\mathrm{5}}{{s}−\mathrm{5}}\mid\right)_{\mathrm{0}} ^{\mathrm{4}} =\:\frac{\mathrm{ln}\:\left(\mathrm{9}\right)}{\mathrm{40}}.\blacktriangle \\ $$
