
Question Number 122904 by Khalmohmmad last updated on 20/Nov/20

$$\left(\mathrm{1}+{i}\right)^{\mathrm{9}} =? \\ $$
Answered by Bird last updated on 20/Nov/20
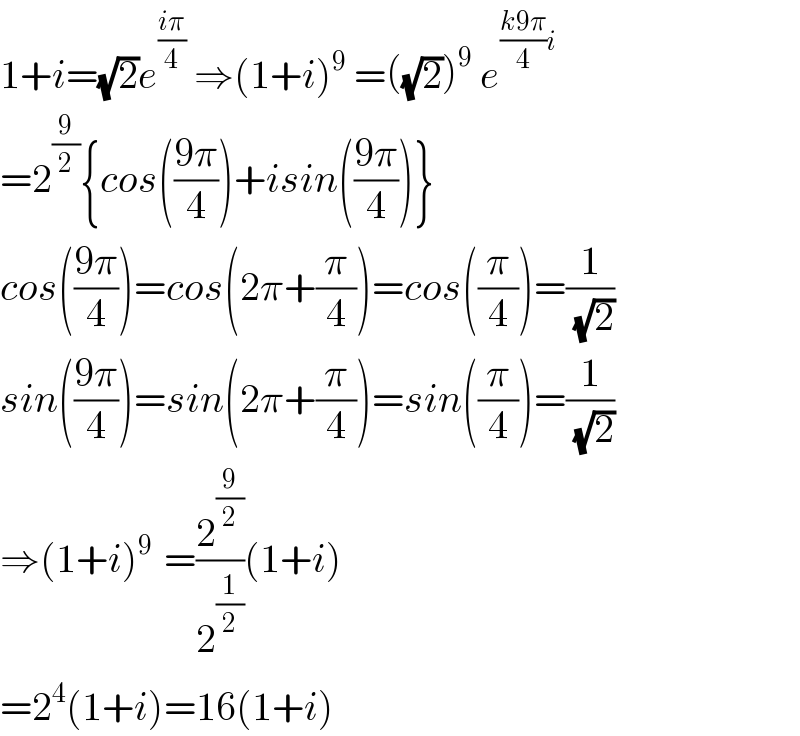
$$\mathrm{1}+{i}=\sqrt{\mathrm{2}}{e}^{\frac{{i}\pi}{\mathrm{4}}} \:\Rightarrow\left(\mathrm{1}+{i}\right)^{\mathrm{9}} \:=\left(\sqrt{\mathrm{2}}\right)^{\mathrm{9}} \:{e}^{\frac{{k}\mathrm{9}\pi}{\mathrm{4}}{i}} \\ $$$$=\mathrm{2}^{\frac{\mathrm{9}}{\mathrm{2}}} \left\{{cos}\left(\frac{\mathrm{9}\pi}{\mathrm{4}}\right)+{isin}\left(\frac{\mathrm{9}\pi}{\mathrm{4}}\right)\right\} \\ $$$${cos}\left(\frac{\mathrm{9}\pi}{\mathrm{4}}\right)={cos}\left(\mathrm{2}\pi+\frac{\pi}{\mathrm{4}}\right)={cos}\left(\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$${sin}\left(\frac{\mathrm{9}\pi}{\mathrm{4}}\right)={sin}\left(\mathrm{2}\pi+\frac{\pi}{\mathrm{4}}\right)={sin}\left(\frac{\pi}{\mathrm{4}}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\left(\mathrm{1}+{i}\right)^{\mathrm{9}\:} \:=\frac{\mathrm{2}^{\frac{\mathrm{9}}{\mathrm{2}}} }{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}}} }\left(\mathrm{1}+{i}\right) \\ $$$$=\mathrm{2}^{\mathrm{4}} \left(\mathrm{1}+{i}\right)=\mathrm{16}\left(\mathrm{1}+{i}\right) \\ $$
Answered by Olaf last updated on 20/Nov/20
![(1+i)^9 = [(√2)e^(i(π/4)) ]^9 = 2^(9/2) e^(i((9π)/4)) = 16(√2)e^(i((π/4)+2π)) = 16(√2)(((1+i)/( (√2)))) = 16(1+i)](Q122911.png)
$$\left(\mathrm{1}+{i}\right)^{\mathrm{9}} \:=\:\left[\sqrt{\mathrm{2}}{e}^{{i}\frac{\pi}{\mathrm{4}}} \right]^{\mathrm{9}} \:=\:\mathrm{2}^{\frac{\mathrm{9}}{\mathrm{2}}} {e}^{{i}\frac{\mathrm{9}\pi}{\mathrm{4}}} \\ $$$$=\:\mathrm{16}\sqrt{\mathrm{2}}{e}^{{i}\left(\frac{\pi}{\mathrm{4}}+\mathrm{2}\pi\right)} \:=\:\mathrm{16}\sqrt{\mathrm{2}}\left(\frac{\mathrm{1}+{i}}{\:\sqrt{\mathrm{2}}}\right)\:=\:\mathrm{16}\left(\mathrm{1}+{i}\right) \\ $$
