
Question Number 122862 by Dwaipayan Shikari last updated on 20/Nov/20
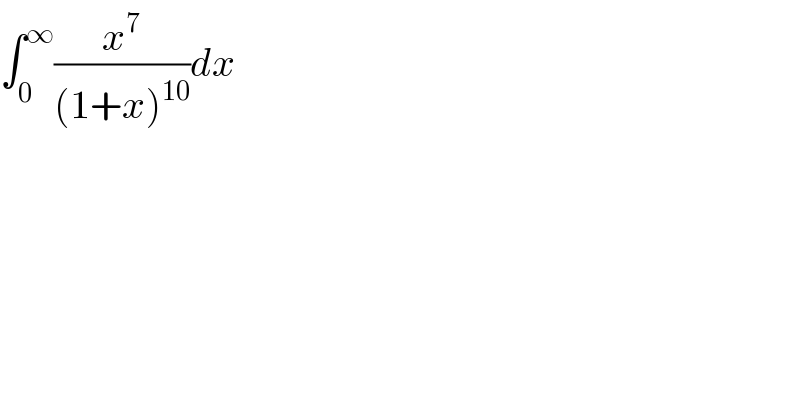
$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{7}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{10}} }{dx} \\ $$
Answered by MJS_new last updated on 20/Nov/20
![=∫_0 ^∞ Σ_(j=3) ^(10) (((−1)^(j+1) ((7),((j−3)) ))/((x+1)^j ))=[Σ_(j=3) ^(10) (((−1)^(j+1) ((7),((j−3)) ))/((j−1)(x+1)^(j−1) ))]_0 ^∞ = =−Σ_(j=3) ^(10) (((−1)^(j+1) ((7),((j−3)) ))/((j−1)))= =(1/2)−(7/3)+((21)/4)−7+((35)/6)−3+(7/8)−(1/9)=(1/(72))](Q122869.png)
$$=\underset{\mathrm{0}} {\overset{\infty} {\int}}\underset{{j}=\mathrm{3}} {\overset{\mathrm{10}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{j}+\mathrm{1}} \begin{pmatrix}{\mathrm{7}}\\{{j}−\mathrm{3}}\end{pmatrix}}{\left({x}+\mathrm{1}\right)^{{j}} }=\left[\underset{{j}=\mathrm{3}} {\overset{\mathrm{10}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{j}+\mathrm{1}} \begin{pmatrix}{\mathrm{7}}\\{{j}−\mathrm{3}}\end{pmatrix}}{\left({j}−\mathrm{1}\right)\left({x}+\mathrm{1}\right)^{{j}−\mathrm{1}} }\right]_{\mathrm{0}} ^{\infty} = \\ $$$$=−\underset{{j}=\mathrm{3}} {\overset{\mathrm{10}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{j}+\mathrm{1}} \begin{pmatrix}{\mathrm{7}}\\{{j}−\mathrm{3}}\end{pmatrix}}{\left({j}−\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{7}}{\mathrm{3}}+\frac{\mathrm{21}}{\mathrm{4}}−\mathrm{7}+\frac{\mathrm{35}}{\mathrm{6}}−\mathrm{3}+\frac{\mathrm{7}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{72}} \\ $$
Commented by Dwaipayan Shikari last updated on 20/Nov/20

$${Great}\:{way}\:{sir}!\: \\ $$
Commented by Dwaipayan Shikari last updated on 20/Nov/20
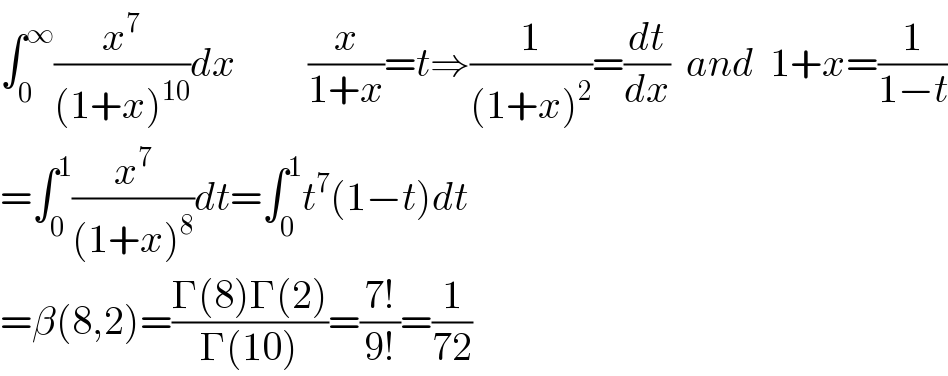
$$\int_{\mathrm{0}} ^{\infty} \frac{{x}^{\mathrm{7}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{10}} }{dx}\:\:\:\:\:\:\:\:\:\frac{{x}}{\mathrm{1}+{x}}={t}\Rightarrow\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\frac{{dt}}{{dx}}\:\:{and}\:\:\mathrm{1}+{x}=\frac{\mathrm{1}}{\mathrm{1}−{t}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{7}} }{\left(\mathrm{1}+{x}\right)^{\mathrm{8}} }{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{7}} \left(\mathrm{1}−{t}\right){dt} \\ $$$$=\beta\left(\mathrm{8},\mathrm{2}\right)=\frac{\Gamma\left(\mathrm{8}\right)\Gamma\left(\mathrm{2}\right)}{\Gamma\left(\mathrm{10}\right)}=\frac{\mathrm{7}!}{\mathrm{9}!}=\frac{\mathrm{1}}{\mathrm{72}} \\ $$
