
Question Number 122854 by Study last updated on 20/Nov/20
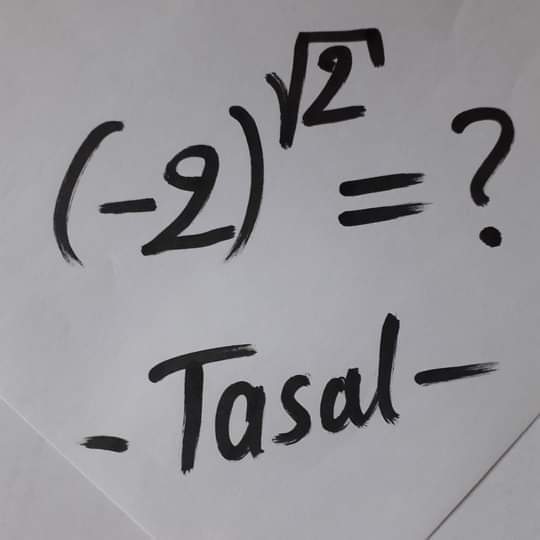
Answered by mathmax by abdo last updated on 20/Nov/20
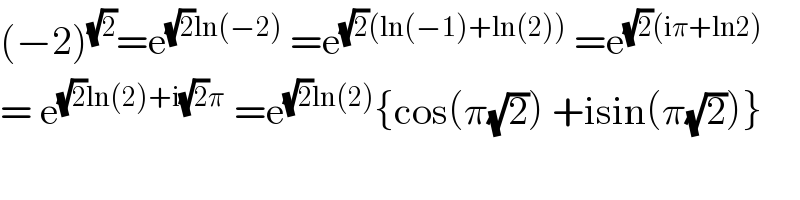
$$\left(−\mathrm{2}\right)^{\sqrt{\mathrm{2}}} =\mathrm{e}^{\sqrt{\mathrm{2}}\mathrm{ln}\left(−\mathrm{2}\right)} \:=\mathrm{e}^{\sqrt{\mathrm{2}}\left(\mathrm{ln}\left(−\mathrm{1}\right)+\mathrm{ln}\left(\mathrm{2}\right)\right)} \:=\mathrm{e}^{\sqrt{\mathrm{2}}\left(\mathrm{i}\pi+\mathrm{ln2}\right)} \\ $$$$=\:\mathrm{e}^{\sqrt{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)+\mathrm{i}\sqrt{\mathrm{2}}\pi} \:=\mathrm{e}^{\sqrt{\mathrm{2}}\mathrm{ln}\left(\mathrm{2}\right)} \left\{\mathrm{cos}\left(\pi\sqrt{\mathrm{2}}\right)\:+\mathrm{isin}\left(\pi\sqrt{\mathrm{2}}\right)\right\} \\ $$
