
Question Number 122848 by ZiYangLee last updated on 20/Nov/20
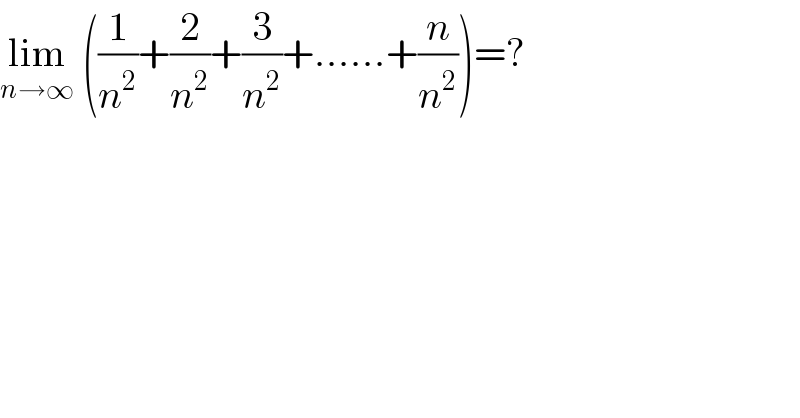
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\frac{\mathrm{2}}{{n}^{\mathrm{2}} }+\frac{\mathrm{3}}{{n}^{\mathrm{2}} }+......+\frac{{n}}{{n}^{\mathrm{2}} }\right)=? \\ $$
Answered by nico last updated on 20/Nov/20
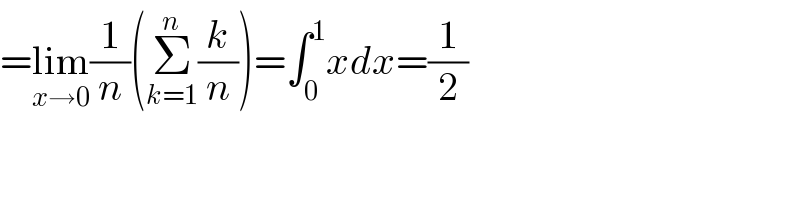
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\left(\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{k}}{{n}}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {xdx}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by mindispower last updated on 20/Nov/20
![=Σ_(0≤k≤n) (k/n^2 )=−(∂/∂x)(1/n^2 )Σe^(kx) ∣_(x=0) =(∂/∂x).(1/n^2 ).((1−(e^x )^(n+1) )/(1−e^x )) =(1/n^2 ).(∂/∂x).e^((nx)/2) .((sh(((n+1)/2)x))/(sh((x/2))))∣_(x=0) =(1/n^2 )lim_(x→0) [(n/2)e^((nx)/2) .((sh(((n+1)/2)x))/(sh((x/2))))+e^(n(x/2)) .[((((n+1)/2)ch(((n+1)/2)x)sh((x/2))−(1/2)ch((x/2))sh(((n+1)/2)x))/(sh^2 ((x/2))))] =(1/n^2 ),(n/2).((n+1)/2).(2/)+1.0 =lim_(n→∞) .(1/n^2 ).((n(n+1))/2)=(1/2)](Q122856.png)
$$=\underset{\mathrm{0}\leqslant{k}\leqslant{n}} {\sum}\frac{{k}}{{n}^{\mathrm{2}} }=−\frac{\partial}{\partial{x}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\Sigma{e}^{{kx}} \mid_{{x}=\mathrm{0}} \\ $$$$=\frac{\partial}{\partial{x}}.\frac{\mathrm{1}}{{n}^{\mathrm{2}} }.\frac{\mathrm{1}−\left({e}^{{x}} \right)^{{n}+\mathrm{1}} }{\mathrm{1}−{e}^{{x}} } \\ $$$$=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }.\frac{\partial}{\partial{x}}.{e}^{\frac{{nx}}{\mathrm{2}}} .\frac{{sh}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)}{{sh}\left(\frac{{x}}{\mathrm{2}}\right)}\mid_{{x}=\mathrm{0}} \\ $$$$ \\ $$$$=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{{n}}{\mathrm{2}}{e}^{\frac{{nx}}{\mathrm{2}}} .\frac{{sh}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)}{{sh}\left(\frac{{x}}{\mathrm{2}}\right)}+{e}^{{n}\frac{{x}}{\mathrm{2}}} .\left[\frac{\frac{{n}+\mathrm{1}}{\mathrm{2}}{ch}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right){sh}\left(\frac{{x}}{\mathrm{2}}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ch}\left(\frac{{x}}{\mathrm{2}}\right){sh}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right)}{{sh}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}\right]\right. \\ $$$$=\frac{\mathrm{1}}{{n}^{\mathrm{2}} },\frac{{n}}{\mathrm{2}}.\frac{{n}+\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2}}{}+\mathrm{1}.\mathrm{0} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}.\frac{\mathrm{1}}{{n}^{\mathrm{2}} }.\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
