Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 122751 by bemath last updated on 19/Nov/20

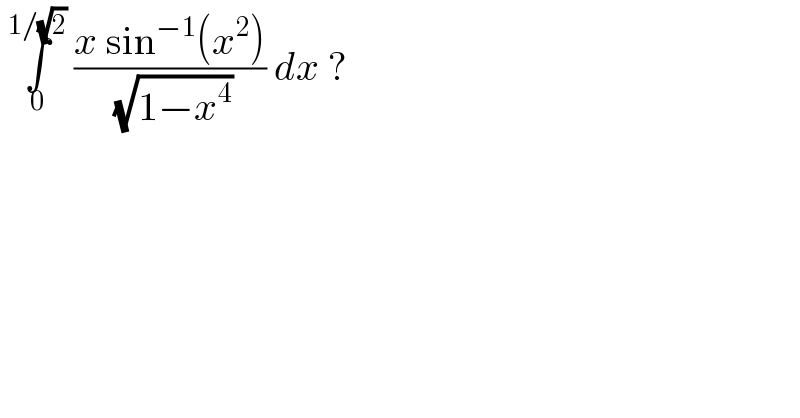
∫_0 ^(1/(√2)) ((x sin^(−1) (x^2 ))/( (√(1−x^4 )))) dx ?

$$\:\underset{\mathrm{0}} {\overset{\mathrm{1}/\sqrt{\mathrm{2}}} {\int}}\:\frac{{x}\:\mathrm{sin}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\:{dx}\:?\: \\ $$

Answered by liberty last updated on 19/Nov/20

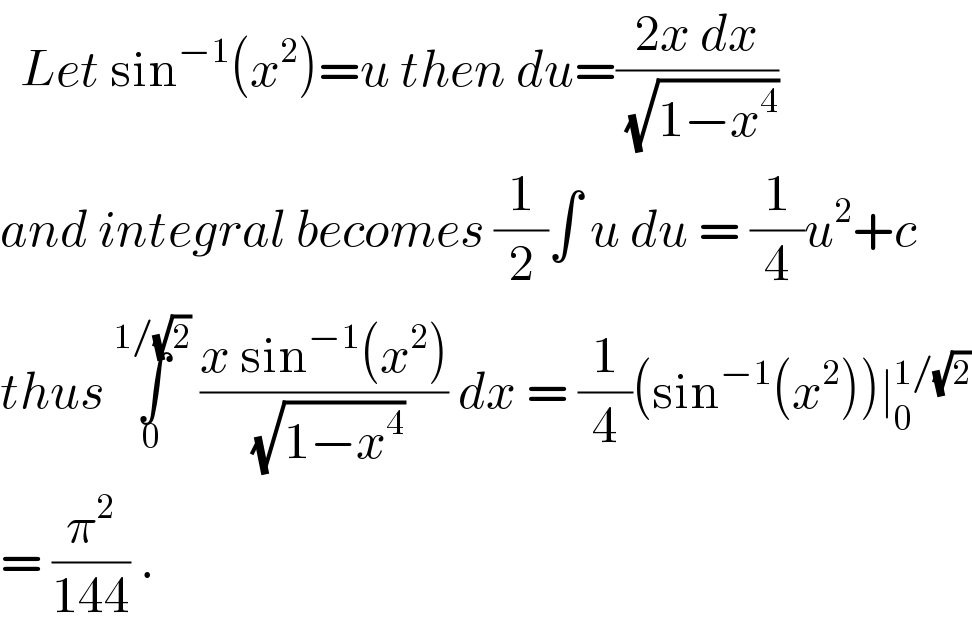
Let sin^(−1) (x^2 )=u then du=((2x dx)/( (√(1−x^4 )))) and integral becomes (1/2)∫ u du = (1/4)u^2 +c thus ∫_0 ^(1/(√2)) ((x sin^(−1) (x^2 ))/( (√(1−x^4 )))) dx = (1/4)(sin^(−1) (x^2 ))∣_0 ^(1/(√2)) = (π^2 /(144)) .

$$\:\:{Let}\:\mathrm{sin}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \right)={u}\:{then}\:{du}=\frac{\mathrm{2}{x}\:{dx}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }} \\ $$$${and}\:{integral}\:{becomes}\:\frac{\mathrm{1}}{\mathrm{2}}\int\:{u}\:{du}\:=\:\frac{\mathrm{1}}{\mathrm{4}}{u}^{\mathrm{2}} +{c} \\ $$$${thus}\:\underset{\mathrm{0}} {\overset{\mathrm{1}/\sqrt{\mathrm{2}}} {\int}}\:\frac{{x}\:\mathrm{sin}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{sin}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \right)\right)\mid_{\mathrm{0}} ^{\mathrm{1}/\sqrt{\mathrm{2}}} \\ $$$$=\:\frac{\pi^{\mathrm{2}} }{\mathrm{144}}\:.\: \\ $$

Answered by Dwaipayan Shikari last updated on 19/Nov/20

∫_0 ^(1/( (√2))) ((xsin^(−1) (x^2 ))/( (√(1−x^4 ))))dx x^2 =t⇒2x=(dt/dx) (1/2)∫_0 ^(1/2) ((sin^(−1) (t))/( (√(1−t^2 ))))dt=(1/4)[(sin^(−1) t)^2 ]_0 ^(1/2) =(1/4).(π^2 /(36))=(π^2 /(144))

$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \frac{{xsin}^{−\mathrm{1}} \left({x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{dx}\:\:\:\:\:\:{x}^{\mathrm{2}} ={t}\Rightarrow\mathrm{2}{x}=\frac{{dt}}{{dx}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \frac{{sin}^{−\mathrm{1}} \left({t}\right)}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt}=\frac{\mathrm{1}}{\mathrm{4}}\left[\left({sin}^{−\mathrm{1}} {t}\right)^{\mathrm{2}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\mathrm{4}}.\frac{\pi^{\mathrm{2}} }{\mathrm{36}}=\frac{\pi^{\mathrm{2}} }{\mathrm{144}} \\ $$

Answered by Bird last updated on 19/Nov/20

I =∫_0 ^(1/( (√2))) ((xarcsin(x^2 ))/( (√(1−x^4 ))))dx we do the changement x^2 =t ⇒2xdx =dt ⇒ I =∫_0 ^(1/2) ((arcsin(t))/( (√(1−t^2 ))))(dt/2) ⇒2I =[arcsin^2 t]_0 ^(1/2) −∫_0 ^(1/2) ((arcsint)/( (√(1−t^2 ))))dt 3I =((π/6))^2 =(π^2 /(36)) ⇒I =(π^2 /(3.36)) =(π^2 /(108))

$${I}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \:\:\:\frac{{xarcsin}\left({x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{dx}\:{we}\:{do}\:{the} \\ $$$${changement}\:{x}^{\mathrm{2}} ={t}\:\Rightarrow\mathrm{2}{xdx}\:={dt}\:\Rightarrow \\ $$$${I}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{{arcsin}\left({t}\right)}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}\frac{{dt}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}{I}\:=\left[{arcsin}^{\mathrm{2}} {t}\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} −\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \:\frac{{arcsint}}{\:\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }}{dt} \\ $$$$\mathrm{3}{I}\:=\left(\frac{\pi}{\mathrm{6}}\right)^{\mathrm{2}} \:=\frac{\pi^{\mathrm{2}} }{\mathrm{36}}\:\Rightarrow{I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{3}.\mathrm{36}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{108}} \\ $$

Commented by liberty last updated on 19/Nov/20

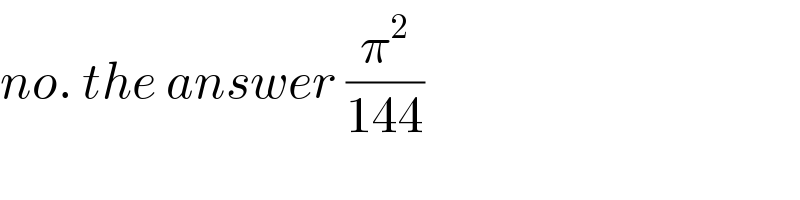
no. the answer (π^2 /(144))

$${no}.\:{the}\:{answer}\:\frac{\pi^{\mathrm{2}} }{\mathrm{144}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com