
Question Number 122555 by ZiYangLee last updated on 18/Nov/20
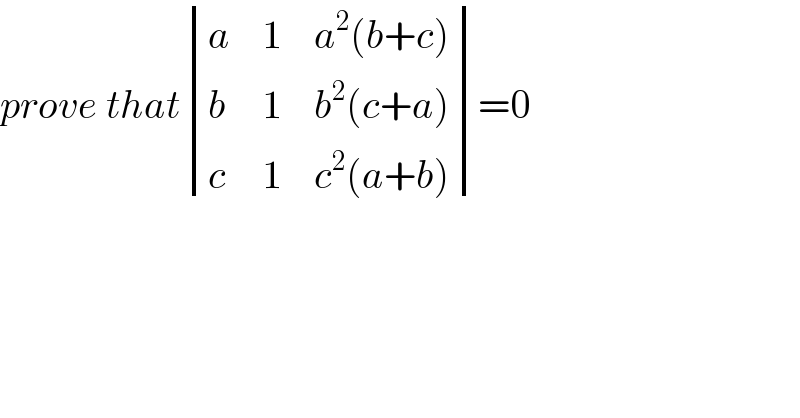
$${prove}\:{that}\begin{vmatrix}{{a}}&{\mathrm{1}}&{{a}^{\mathrm{2}} \left({b}+{c}\right)}\\{{b}}&{\mathrm{1}}&{{b}^{\mathrm{2}} \left({c}+{a}\right)}\\{{c}}&{\mathrm{1}}&{{c}^{\mathrm{2}} \left({a}+{b}\right)}\end{vmatrix}=\mathrm{0} \\ $$
Commented by bramlexs22 last updated on 18/Nov/20
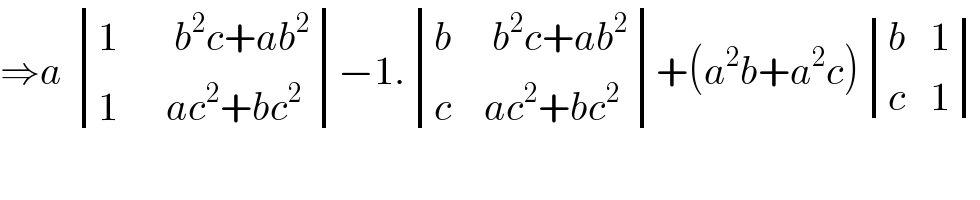
$$\Rightarrow{a}\:\begin{vmatrix}{\mathrm{1}\:\:\:\:\:\:\:{b}^{\mathrm{2}} {c}+{ab}^{\mathrm{2}} }\\{\mathrm{1}\:\:\:\:\:\:{ac}^{\mathrm{2}} +{bc}^{\mathrm{2}} }\end{vmatrix}−\mathrm{1}.\begin{vmatrix}{{b}\:\:\:\:\:{b}^{\mathrm{2}} {c}+{ab}^{\mathrm{2}} }\\{{c}\:\:\:\:{ac}^{\mathrm{2}} +{bc}^{\mathrm{2}} }\end{vmatrix}+\left({a}^{\mathrm{2}} {b}+{a}^{\mathrm{2}} {c}\right)\begin{vmatrix}{{b}\:\:\:\mathrm{1}}\\{{c}\:\:\:\mathrm{1}}\end{vmatrix} \\ $$$$ \\ $$
Answered by $@y@m last updated on 18/Nov/20
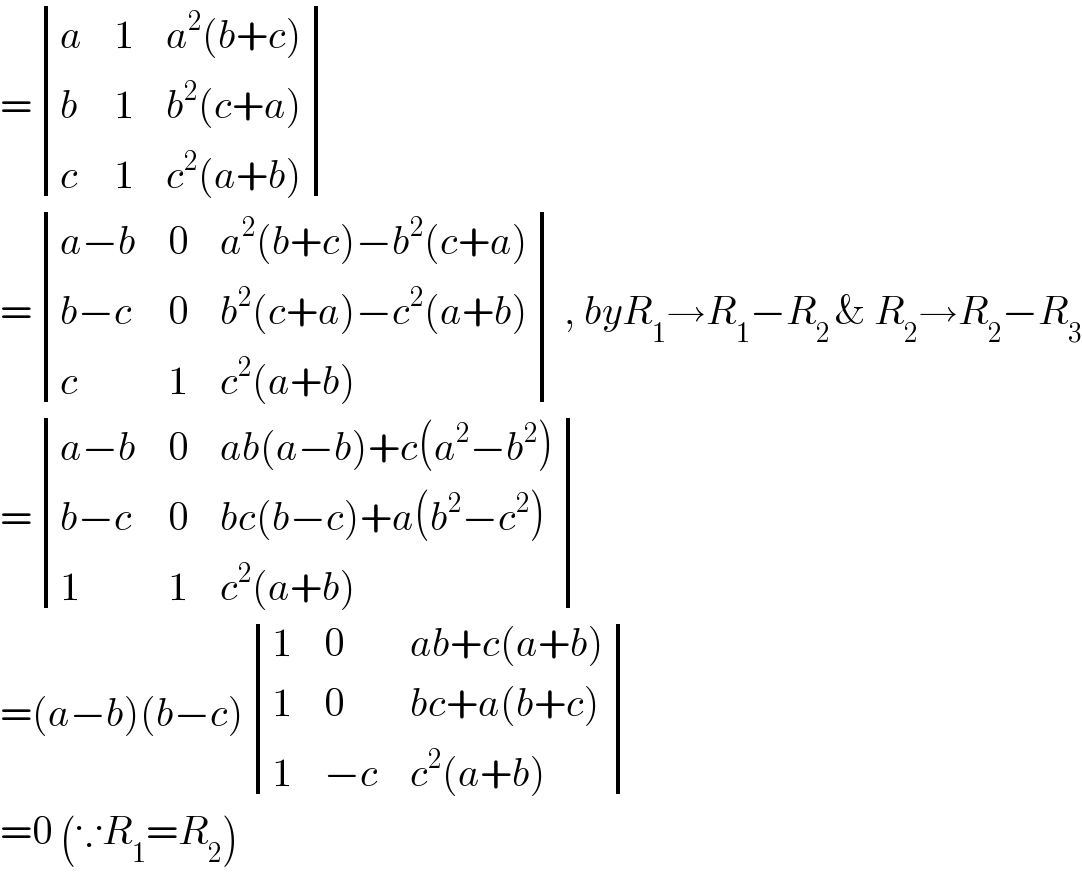
$$=\begin{vmatrix}{{a}}&{\mathrm{1}}&{{a}^{\mathrm{2}} \left({b}+{c}\right)}\\{{b}}&{\mathrm{1}}&{{b}^{\mathrm{2}} \left({c}+{a}\right)}\\{{c}}&{\mathrm{1}}&{{c}^{\mathrm{2}} \left({a}+{b}\right)}\end{vmatrix} \\ $$$$=\begin{vmatrix}{{a}−{b}}&{\mathrm{0}}&{{a}^{\mathrm{2}} \left({b}+{c}\right)−{b}^{\mathrm{2}} \left({c}+{a}\right)}\\{{b}−{c}}&{\mathrm{0}}&{{b}^{\mathrm{2}} \left({c}+{a}\right)−{c}^{\mathrm{2}} \left({a}+{b}\right)}\\{{c}}&{\mathrm{1}}&{{c}^{\mathrm{2}} \left({a}+{b}\right)}\end{vmatrix}\:,\:{byR}_{\mathrm{1}} \rightarrow{R}_{\mathrm{1}} −{R}_{\mathrm{2}\:} \&\:{R}_{\mathrm{2}} \rightarrow{R}_{\mathrm{2}} −{R}_{\mathrm{3}} \\ $$$$=\begin{vmatrix}{{a}−{b}}&{\mathrm{0}}&{{ab}\left({a}−{b}\right)+{c}\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)}\\{{b}−{c}}&{\mathrm{0}}&{{bc}\left({b}−{c}\right)+{a}\left({b}^{\mathrm{2}} −{c}^{\mathrm{2}} \right)}\\{\mathrm{1}}&{\mathrm{1}}&{{c}^{\mathrm{2}} \left({a}+{b}\right)}\end{vmatrix}\:\: \\ $$$$=\left({a}−{b}\right)\left({b}−{c}\right)\begin{vmatrix}{\mathrm{1}}&{\mathrm{0}}&{{ab}+{c}\left({a}+{b}\right)}\\{\mathrm{1}}&{\mathrm{0}}&{{bc}+{a}\left({b}+{c}\right)}\\{\mathrm{1}}&{−{c}}&{{c}^{\mathrm{2}} \left({a}+{b}\right)}\end{vmatrix}\:\: \\ $$$$=\mathrm{0}\:\left(\because{R}_{\mathrm{1}} ={R}_{\mathrm{2}} \right) \\ $$
Commented by ZiYangLee last updated on 18/Nov/20
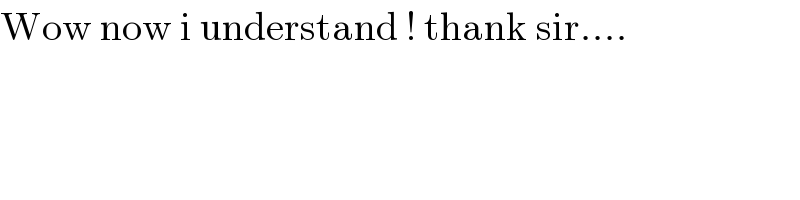
$$\mathrm{Wow}\:\mathrm{now}\:\mathrm{i}\:\mathrm{understand}\:!\:\mathrm{thank}\:\mathrm{sir}.... \\ $$
Answered by MJS_new last updated on 18/Nov/20
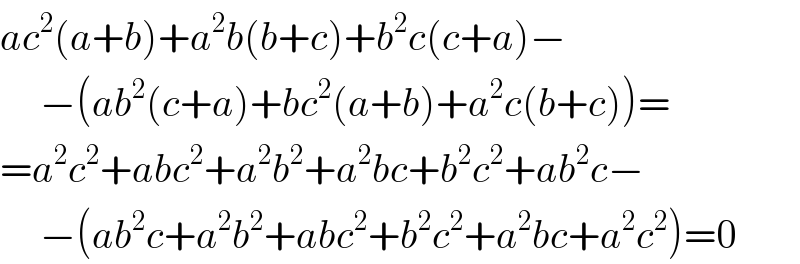
$${ac}^{\mathrm{2}} \left({a}+{b}\right)+{a}^{\mathrm{2}} {b}\left({b}+{c}\right)+{b}^{\mathrm{2}} {c}\left({c}+{a}\right)− \\ $$$$\:\:\:\:\:−\left({ab}^{\mathrm{2}} \left({c}+{a}\right)+{bc}^{\mathrm{2}} \left({a}+{b}\right)+{a}^{\mathrm{2}} {c}\left({b}+{c}\right)\right)= \\ $$$$={a}^{\mathrm{2}} {c}^{\mathrm{2}} +{abc}^{\mathrm{2}} +{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{a}^{\mathrm{2}} {bc}+{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{ab}^{\mathrm{2}} {c}− \\ $$$$\:\:\:\:\:−\left({ab}^{\mathrm{2}} {c}+{a}^{\mathrm{2}} {b}^{\mathrm{2}} +{abc}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{a}^{\mathrm{2}} {bc}+{a}^{\mathrm{2}} {c}^{\mathrm{2}} \right)=\mathrm{0} \\ $$
