
Question Number 122523 by greg_ed last updated on 17/Nov/20
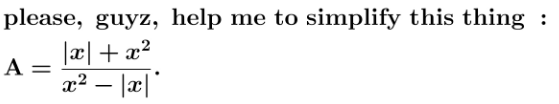
Answered by 676597498 last updated on 17/Nov/20
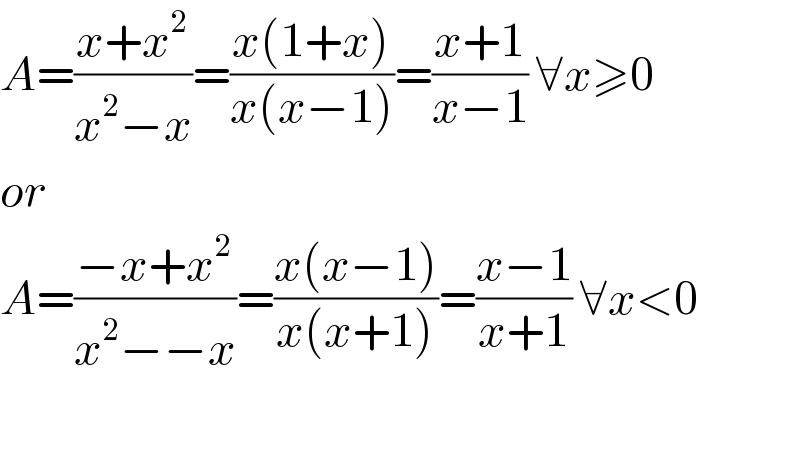
$${A}=\frac{{x}+{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −{x}}=\frac{{x}\left(\mathrm{1}+{x}\right)}{{x}\left({x}−\mathrm{1}\right)}=\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\:\forall{x}\geqslant\mathrm{0} \\ $$$${or} \\ $$$${A}=\frac{−{x}+{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} −−{x}}=\frac{{x}\left({x}−\mathrm{1}\right)}{{x}\left({x}+\mathrm{1}\right)}=\frac{{x}−\mathrm{1}}{{x}+\mathrm{1}}\:\forall{x}<\mathrm{0} \\ $$$$ \\ $$
Commented by greg_ed last updated on 17/Nov/20

$$\mathrm{thank}\:\mathrm{u} \\ $$
Commented by MJS_new last updated on 17/Nov/20
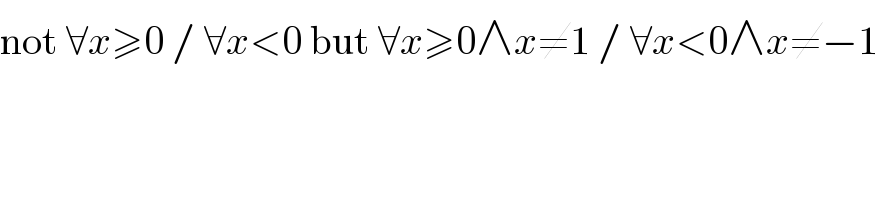
$$\mathrm{not}\:\forall{x}\geqslant\mathrm{0}\:/\:\forall{x}<\mathrm{0}\:\mathrm{but}\:\forall{x}\geqslant\mathrm{0}\wedge{x}\neq\mathrm{1}\:/\:\forall{x}<\mathrm{0}\wedge{x}\neq−\mathrm{1} \\ $$
Answered by mr W last updated on 17/Nov/20
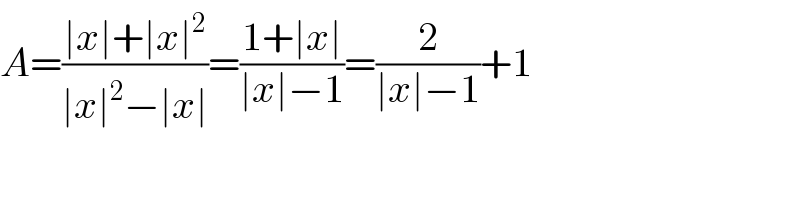
$${A}=\frac{\mid{x}\mid+\mid{x}\mid^{\mathrm{2}} }{\mid{x}\mid^{\mathrm{2}} −\mid{x}\mid}=\frac{\mathrm{1}+\mid{x}\mid}{\mid{x}\mid−\mathrm{1}}=\frac{\mathrm{2}}{\mid{x}\mid−\mathrm{1}}+\mathrm{1} \\ $$
Commented by greg_ed last updated on 17/Nov/20

$$\mathrm{ok}\:! \\ $$
