
Question Number 122506 by mathace last updated on 17/Nov/20
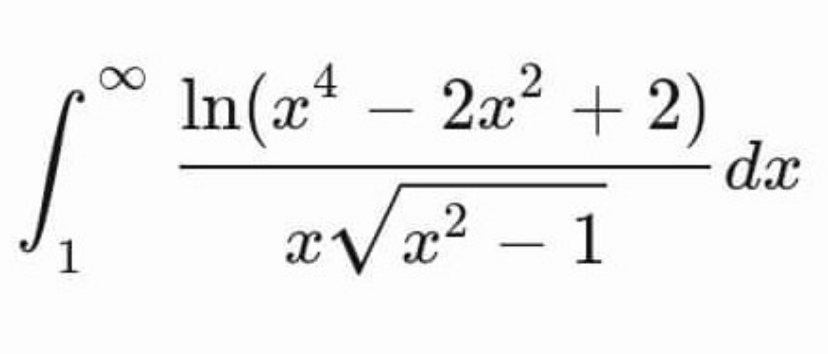
Answered by TANMAY PANACEA last updated on 17/Nov/20

$$\int\frac{{ln}\left(\mathrm{1}+\left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} \right)}{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}{dx} \\ $$$${x}={seca} \\ $$$$\int\frac{{ln}\left(\mathrm{1}+{tan}^{\mathrm{4}} {a}\right)}{{seca}\:{tana}}{secatana}\:{da} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{tan}^{\mathrm{4}} {a}\right){da} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{tan}^{\mathrm{4}} {a}}\right){da} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{tan}^{\mathrm{4}} {a}\right)−\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {lntana}\:{da} \\ $$$${I}={I}−\mathrm{4}{J}\rightarrow{J}=\mathrm{0} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\mathrm{1}+{tan}^{\mathrm{4}} {a}\right){da} \\ $$$$\boldsymbol{{not}}\:\boldsymbol{{reaching}}\:\boldsymbol{{to}}\:\boldsymbol{{goal}} \\ $$
Commented by mathace last updated on 17/Nov/20

$${No}.{It}\:{has}\:{a}\:{finite}\:{value}.\:{Check}\:{your}\:\mathrm{4}{th}\:{line}. \\ $$
Commented by TANMAY PANACEA last updated on 17/Nov/20

$${thank}\:{you}\:{sir} \\ $$
Commented by mindispower last updated on 17/Nov/20

$${withe}\:{pleasur}\: \\ $$
Commented by Dwaipayan Shikari last updated on 18/Nov/20
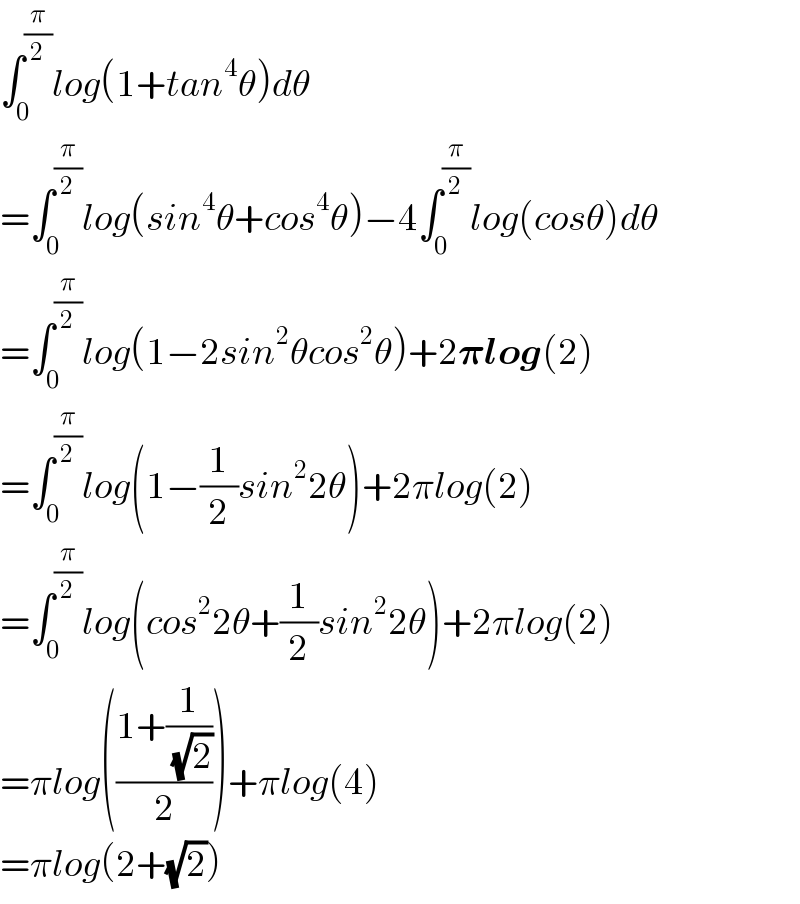
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\mathrm{1}+{tan}^{\mathrm{4}} \theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({sin}^{\mathrm{4}} \theta+{cos}^{\mathrm{4}} \theta\right)−\mathrm{4}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({cos}\theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \theta{cos}^{\mathrm{2}} \theta\right)+\mathrm{2}\boldsymbol{\pi{log}}\left(\mathrm{2}\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \mathrm{2}\theta\right)+\mathrm{2}\pi{log}\left(\mathrm{2}\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({cos}^{\mathrm{2}} \mathrm{2}\theta+\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \mathrm{2}\theta\right)+\mathrm{2}\pi{log}\left(\mathrm{2}\right) \\ $$$$=\pi{log}\left(\frac{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\mathrm{2}}\right)+\pi{log}\left(\mathrm{4}\right) \\ $$$$=\pi{log}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right) \\ $$
Commented by mathace last updated on 18/Nov/20

$${Well}\:{done},{sir}. \\ $$
Commented by Dwaipayan Shikari last updated on 18/Nov/20
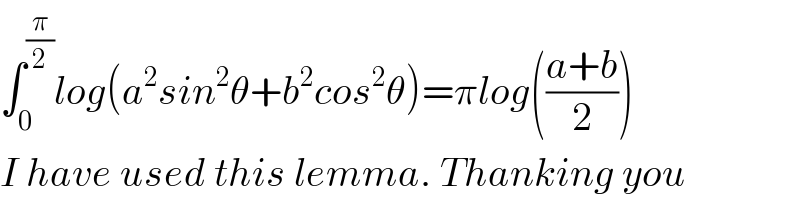
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {log}\left({a}^{\mathrm{2}} {sin}^{\mathrm{2}} \theta+{b}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta\right)=\pi{log}\left(\frac{{a}+{b}}{\mathrm{2}}\right) \\ $$$${I}\:{have}\:{used}\:{this}\:{lemma}.\:{Thanking}\:{you} \\ $$
Commented by mnjuly1970 last updated on 18/Nov/20
$${thank}\:{you} \\ $$$$\:{excellent}.{bravo}... \\ $$
