
Question Number 122467 by Dwaipayan Shikari last updated on 17/Nov/20
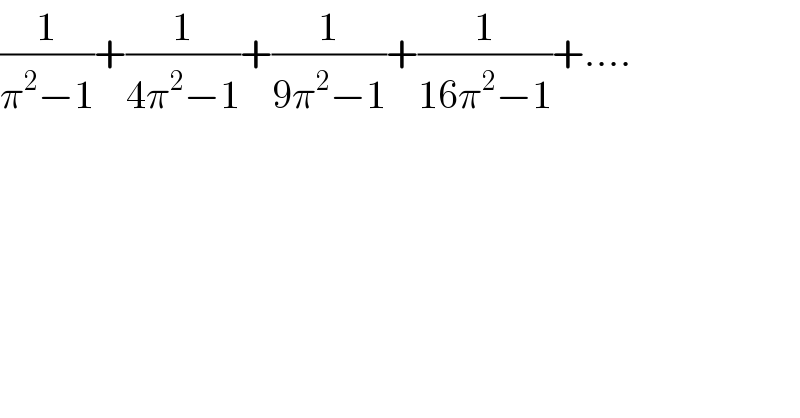
$$\frac{\mathrm{1}}{\pi^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{4}\pi^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{9}\pi^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{16}\pi^{\mathrm{2}} −\mathrm{1}}+.... \\ $$
Commented by Dwaipayan Shikari last updated on 17/Nov/20
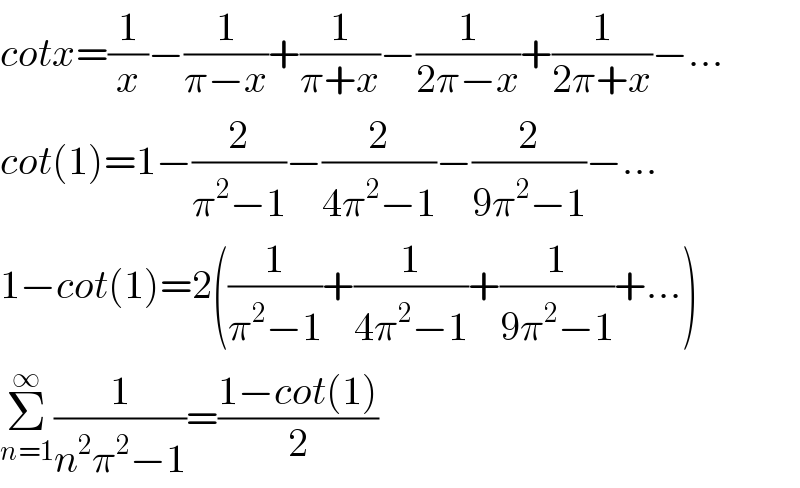
$${cotx}=\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{\pi−{x}}+\frac{\mathrm{1}}{\pi+{x}}−\frac{\mathrm{1}}{\mathrm{2}\pi−{x}}+\frac{\mathrm{1}}{\mathrm{2}\pi+{x}}−... \\ $$$${cot}\left(\mathrm{1}\right)=\mathrm{1}−\frac{\mathrm{2}}{\pi^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{4}\pi^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{9}\pi^{\mathrm{2}} −\mathrm{1}}−... \\ $$$$\mathrm{1}−{cot}\left(\mathrm{1}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{\pi^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{4}\pi^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{9}\pi^{\mathrm{2}} −\mathrm{1}}+...\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \pi^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{1}−{cot}\left(\mathrm{1}\right)}{\mathrm{2}} \\ $$
Answered by mnjuly1970 last updated on 17/Nov/20
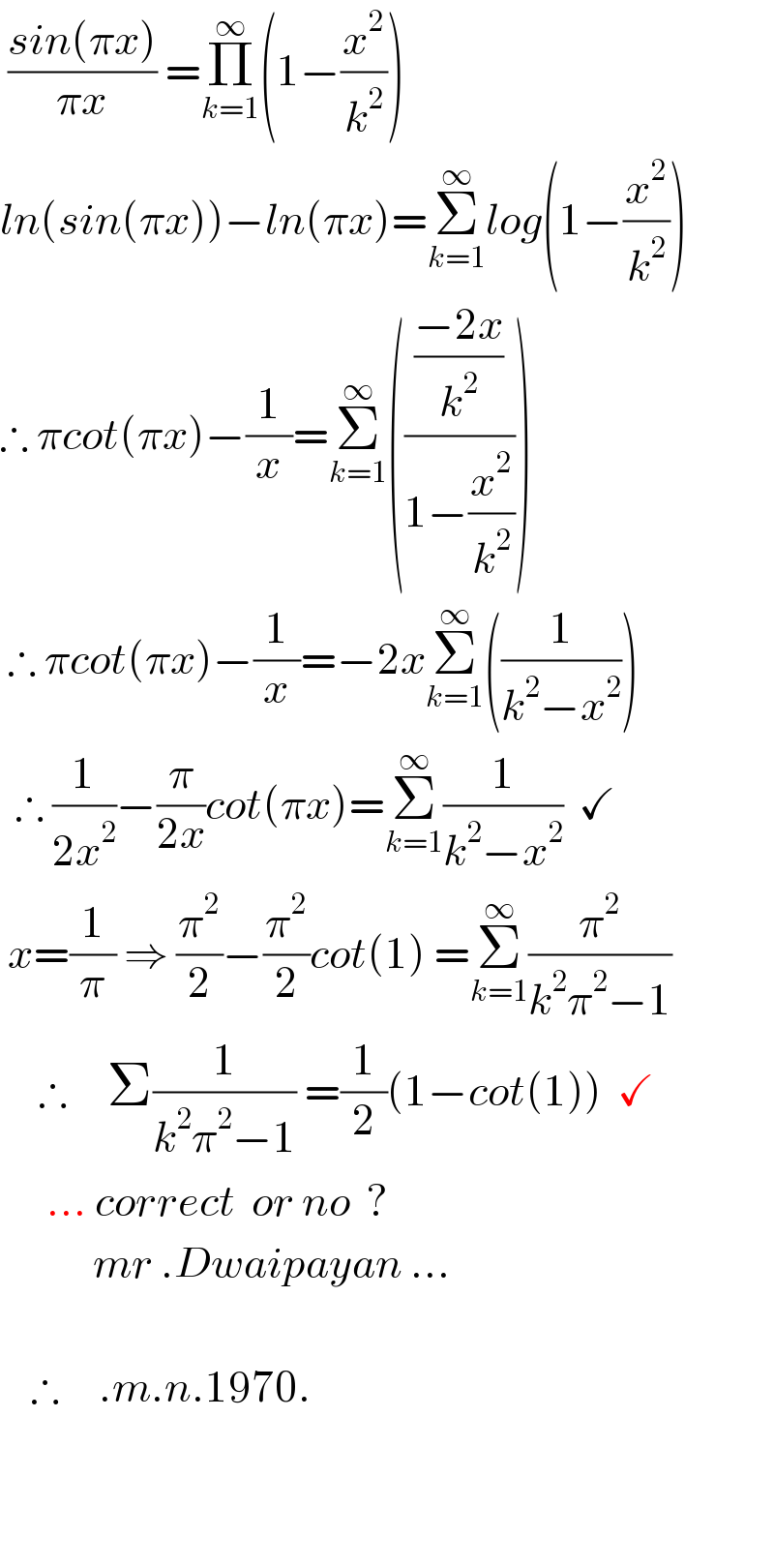
$$\:\frac{{sin}\left(\pi{x}\right)}{\pi{x}}\:=\underset{{k}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{k}^{\mathrm{2}} }\right) \\ $$$${ln}\left({sin}\left(\pi{x}\right)\right)−{ln}\left(\pi{x}\right)=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{log}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{k}^{\mathrm{2}} }\right) \\ $$$$\therefore\:\pi{cot}\left(\pi{x}\right)−\frac{\mathrm{1}}{{x}}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\frac{−\mathrm{2}{x}}{{k}^{\mathrm{2}} }}{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{k}^{\mathrm{2}} }}\right) \\ $$$$\:\therefore\:\pi{cot}\left(\pi{x}\right)−\frac{\mathrm{1}}{{x}}=−\mathrm{2}{x}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{k}^{\mathrm{2}} −{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\therefore\:\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }−\frac{\pi}{\mathrm{2}{x}}{cot}\left(\pi{x}\right)=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:\:\checkmark \\ $$$$\:{x}=\frac{\mathrm{1}}{\pi}\:\Rightarrow\:\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\frac{\pi^{\mathrm{2}} }{\mathrm{2}}{cot}\left(\mathrm{1}\right)\:=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\pi^{\mathrm{2}} }{{k}^{\mathrm{2}} \pi^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:\:\:\:\:\therefore\:\:\:\:\:\Sigma\frac{\mathrm{1}}{{k}^{\mathrm{2}} \pi^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{cot}\left(\mathrm{1}\right)\right)\:\:\checkmark \\ $$$$\:\:\:\:\:\:...\:{correct}\:\:{or}\:{no}\:\:? \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:{mr}\:.{Dwaipayan}\:... \\ $$$$ \\ $$$$\:\:\:\:\therefore\:\:\:\:\:.{m}.{n}.\mathrm{1970}. \\ $$$$\: \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
Commented by Dwaipayan Shikari last updated on 17/Nov/20
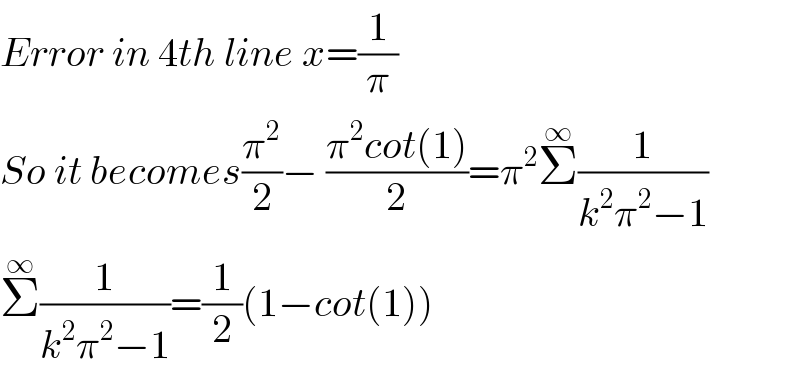
$${Error}\:{in}\:\mathrm{4}{th}\:{line}\:{x}=\frac{\mathrm{1}}{\pi} \\ $$$${So}\:{it}\:{becomes}\frac{\pi^{\mathrm{2}} }{\mathrm{2}}−\:\frac{\pi^{\mathrm{2}} {cot}\left(\mathrm{1}\right)}{\mathrm{2}}=\pi^{\mathrm{2}} \overset{\infty} {\sum}\frac{\mathrm{1}}{{k}^{\mathrm{2}} \pi^{\mathrm{2}} −\mathrm{1}} \\ $$$$\overset{\infty} {\sum}\frac{\mathrm{1}}{{k}^{\mathrm{2}} \pi^{\mathrm{2}} −\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{cot}\left(\mathrm{1}\right)\right) \\ $$
Commented by Dwaipayan Shikari last updated on 17/Nov/20

$${Thanking}\:{you}\:{for}\:{Interacting}\:{with}\:{this}\:{Problem} \\ $$
Commented by mnjuly1970 last updated on 17/Nov/20
$$\:\:{thank}\:\:{you}\:\:{so}\:{much}... \\ $$
Commented by mnjuly1970 last updated on 17/Nov/20

$${excuse}\:{me}\:{mr}\:{payan}.{but} \\ $$$$\:\:{i}\:{couldent}\:{find}\:{any}\:{error} \\ $$$$\:{in}\:\mathrm{4}{th}\:{line}\:.\:{i}\:{differentiated} \\ $$$$\:{both}\:{sides}\:{and}\:{simplified}\:{it}.\:... \\ $$
Commented by mnjuly1970 last updated on 17/Nov/20
$$\:{i}\:{am}\:{checking}\:{it}. \\ $$
Commented by mnjuly1970 last updated on 17/Nov/20
$${please}\:{review}\:{and}\:{recheck}. \\ $$$$\: \\ $$
Commented by Dwaipayan Shikari last updated on 17/Nov/20

$${You}\:{have}\:{edited}\:{many}\:{times}\:{ago}.\:{there}\:{is}\:{no}\:{mistake}\:{now} \\ $$$$\left.{sir}?\::\right) \\ $$$${You}\:{are}\:{wondering}\:{about}\:{the}\:{mistake}\: \\ $$$$\left.{But}\:{actually}\:{there}\:{is}\:{no}\:{mistake}\:\::\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 17/Nov/20

$${you}\:{are}\:{also}\:{funny}\:{person}.\:{joke}\:{is}\:{also}\:{an}\:{aspect} \\ $$$${of}\:{mathematics}\:. \\ $$$${i}\:{think}\:{you}\:{are}\:{many}\:{years}\:{youngers} \\ $$$${than}\:{me}\:. \\ $$$${by}\:{the}\:{way}\:,{you}\:{have}\:{a}\:{good}\:{future} \\ $$$${in}\:{math}.\:{good}\:{luck}\:{young}\:{man}. \\ $$
Commented by Dwaipayan Shikari last updated on 17/Nov/20

$${My}\:{age}\:{is}\:{e}^{\mathrm{2}.\mathrm{82}} \\ $$
Commented by mnjuly1970 last updated on 18/Nov/20
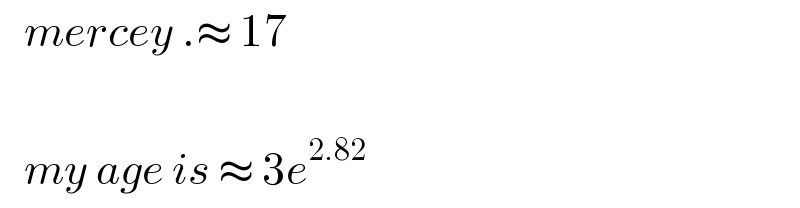
$$\:\:\:{mercey}\:.\approx\:\mathrm{17}\: \\ $$$$\:\:\:\:\:\: \\ $$$$\:\:\:{my}\:{age}\:{is}\:\approx\:\mathrm{3}{e}^{\mathrm{2}.\mathrm{82}} \:\:\:\: \\ $$
