
Question Number 122399 by ajfour last updated on 16/Nov/20
Commented by ajfour last updated on 16/Nov/20

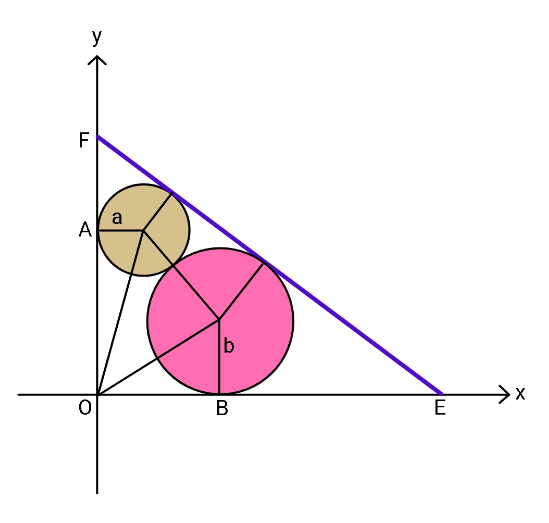
$${Find}\:{in}\:{terms}\:{of}\:{radii}\:{a}\:{and}\:{b} \\ $$$${the}\:{minimum}\:{length}\:{of}\:{common} \\ $$$${tangent}\:{EF}\:{between}\:{the}\:{axes}. \\ $$
Answered by mr W last updated on 16/Nov/20
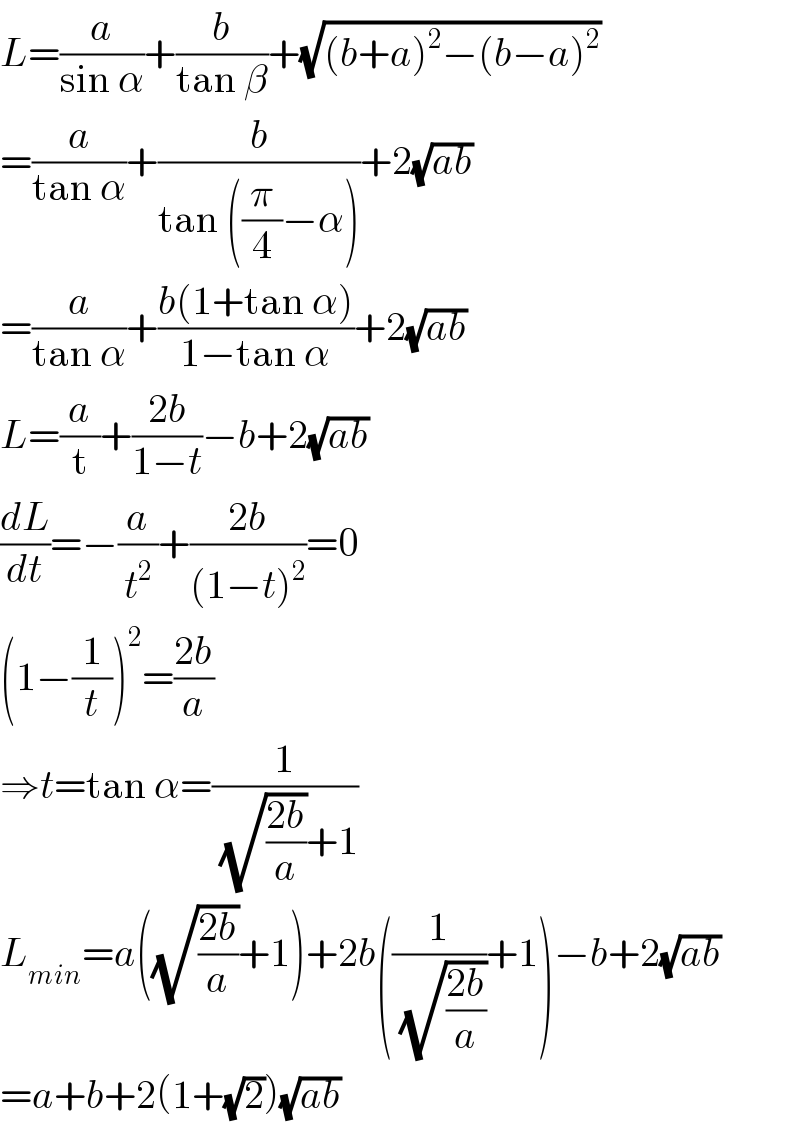
$${L}=\frac{{a}}{\mathrm{sin}\:\alpha}+\frac{{b}}{\mathrm{tan}\:\beta}+\sqrt{\left({b}+{a}\right)^{\mathrm{2}} −\left({b}−{a}\right)^{\mathrm{2}} } \\ $$$$=\frac{{a}}{\mathrm{tan}\:\alpha}+\frac{{b}}{\mathrm{tan}\:\left(\frac{\pi}{\mathrm{4}}−\alpha\right)}+\mathrm{2}\sqrt{{ab}} \\ $$$$=\frac{{a}}{\mathrm{tan}\:\alpha}+\frac{{b}\left(\mathrm{1}+\mathrm{tan}\:\alpha\right)}{\mathrm{1}−\mathrm{tan}\:\alpha}+\mathrm{2}\sqrt{{ab}} \\ $$$${L}=\frac{{a}}{\mathrm{t}}+\frac{\mathrm{2}{b}}{\mathrm{1}−{t}}−{b}+\mathrm{2}\sqrt{{ab}} \\ $$$$\frac{{dL}}{{dt}}=−\frac{{a}}{{t}^{\mathrm{2}} }+\frac{\mathrm{2}{b}}{\left(\mathrm{1}−{t}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} =\frac{\mathrm{2}{b}}{{a}} \\ $$$$\Rightarrow{t}=\mathrm{tan}\:\alpha=\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{2}{b}}{{a}}}+\mathrm{1}} \\ $$$${L}_{{min}} ={a}\left(\sqrt{\frac{\mathrm{2}{b}}{{a}}}+\mathrm{1}\right)+\mathrm{2}{b}\left(\frac{\mathrm{1}}{\:\sqrt{\frac{\mathrm{2}{b}}{{a}}}}+\mathrm{1}\right)−{b}+\mathrm{2}\sqrt{{ab}} \\ $$$$={a}+{b}+\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\sqrt{{ab}} \\ $$
Commented by ajfour last updated on 16/Nov/20
$${thanks}\:{for}\:{solving}\:{sir}! \\ $$
Answered by ajfour last updated on 16/Nov/20
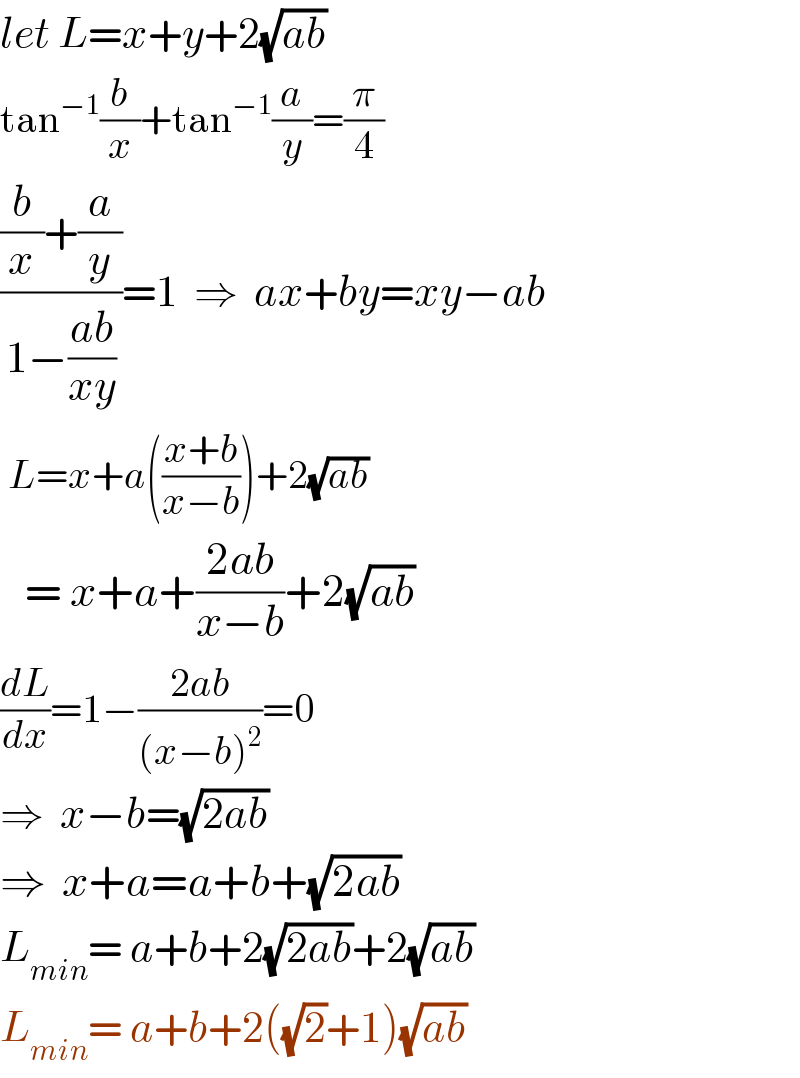
$${let}\:{L}={x}+{y}+\mathrm{2}\sqrt{{ab}} \\ $$$$\mathrm{tan}^{−\mathrm{1}} \frac{{b}}{{x}}+\mathrm{tan}^{−\mathrm{1}} \frac{{a}}{{y}}=\frac{\pi}{\mathrm{4}} \\ $$$$\frac{\frac{{b}}{{x}}+\frac{{a}}{{y}}}{\mathrm{1}−\frac{{ab}}{{xy}}}=\mathrm{1}\:\:\Rightarrow\:\:{ax}+{by}={xy}−{ab} \\ $$$$\:{L}={x}+{a}\left(\frac{{x}+{b}}{{x}−{b}}\right)+\mathrm{2}\sqrt{{ab}} \\ $$$$\:\:\:=\:{x}+{a}+\frac{\mathrm{2}{ab}}{{x}−{b}}+\mathrm{2}\sqrt{{ab}} \\ $$$$\frac{{dL}}{{dx}}=\mathrm{1}−\frac{\mathrm{2}{ab}}{\left({x}−{b}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\Rightarrow\:\:{x}−{b}=\sqrt{\mathrm{2}{ab}}\:\:\: \\ $$$$\Rightarrow\:\:{x}+{a}={a}+{b}+\sqrt{\mathrm{2}{ab}} \\ $$$${L}_{{min}} =\:{a}+{b}+\mathrm{2}\sqrt{\mathrm{2}{ab}}+\mathrm{2}\sqrt{{ab}} \\ $$$${L}_{{min}} =\:{a}+{b}+\mathrm{2}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\sqrt{{ab}}\: \\ $$
