
Question Number 122349 by liberty last updated on 16/Nov/20
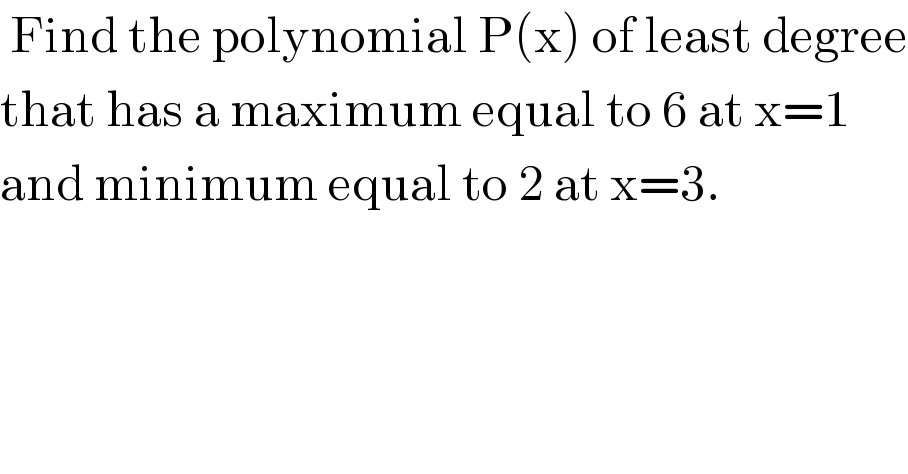
$$\:\mathrm{Find}\:\mathrm{the}\:\mathrm{polynomial}\:\mathrm{P}\left(\mathrm{x}\right)\:\mathrm{of}\:\mathrm{least}\:\mathrm{degree} \\ $$$$\mathrm{that}\:\mathrm{has}\:\mathrm{a}\:\mathrm{maximum}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{6}\:\mathrm{at}\:\mathrm{x}=\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{minimum}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{2}\:\mathrm{at}\:\mathrm{x}=\mathrm{3}.\: \\ $$
Commented by benjo_mathlover last updated on 17/Nov/20

$${my}\:{answer}\::\: \\ $$$${the}\:{polynomial}\:{of}\:{the}\:{least}\:{degree} \\ $$$${with}\:{roots}\:{x}_{\mathrm{1}} =\mathrm{1}\:{and}\:{x}_{\mathrm{2}} =\mathrm{3}\:{has}\:{the}\: \\ $$$${form}\:{a}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right).\:{Hence}\: \\ $$$${P}\:'\left({x}\right)={a}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)={a}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right) \\ $$$${Since}\:{at}\:{the}\:{point}\:{x}=\mathrm{1}\:{there}\:{must}\:{be} \\ $$$${P}\left(\mathrm{1}\right)=\mathrm{6}\:,\:{we}\:{have}\: \\ $$$${P}\left({x}\right)=\underset{\mathrm{1}} {\overset{{x}} {\int}}{P}\:'\left({x}\right)\:{dx}\:+\:\mathrm{6}\: \\ $$$${P}\left({x}\right)=\:{a}\underset{\mathrm{1}} {\overset{{x}} {\int}}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right){dx}+\mathrm{6}\: \\ $$$${P}\left({x}\right)=\:{a}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}−\frac{\mathrm{4}}{\mathrm{3}}\right)+\mathrm{6}. \\ $$$${The}\:{coefficient}\:{a}\:{is}\:{determined} \\ $$$${from}\:{the}\:{condition}\:{P}\left(\mathrm{3}\right)=\mathrm{2},\:{whence} \\ $$$${a}\:=\mathrm{3}\:,\:{Hence}\:{P}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{2}. \\ $$
Answered by mr W last updated on 17/Nov/20
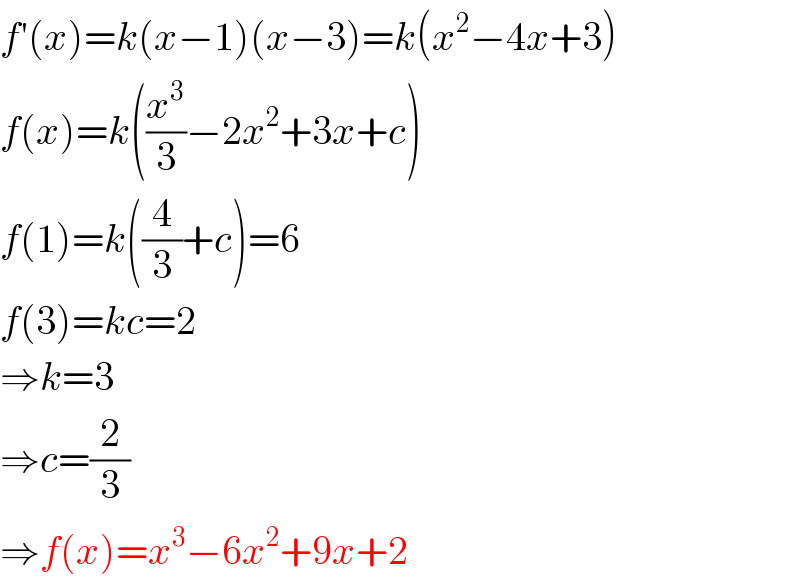
$${f}'\left({x}\right)={k}\left({x}−\mathrm{1}\right)\left({x}−\mathrm{3}\right)={k}\left({x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{3}\right) \\ $$$${f}\left({x}\right)={k}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+{c}\right) \\ $$$${f}\left(\mathrm{1}\right)={k}\left(\frac{\mathrm{4}}{\mathrm{3}}+{c}\right)=\mathrm{6} \\ $$$${f}\left(\mathrm{3}\right)={kc}=\mathrm{2} \\ $$$$\Rightarrow{k}=\mathrm{3} \\ $$$$\Rightarrow{c}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{f}\left({x}\right)={x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} +\mathrm{9}{x}+\mathrm{2} \\ $$
Commented by mr W last updated on 16/Nov/20
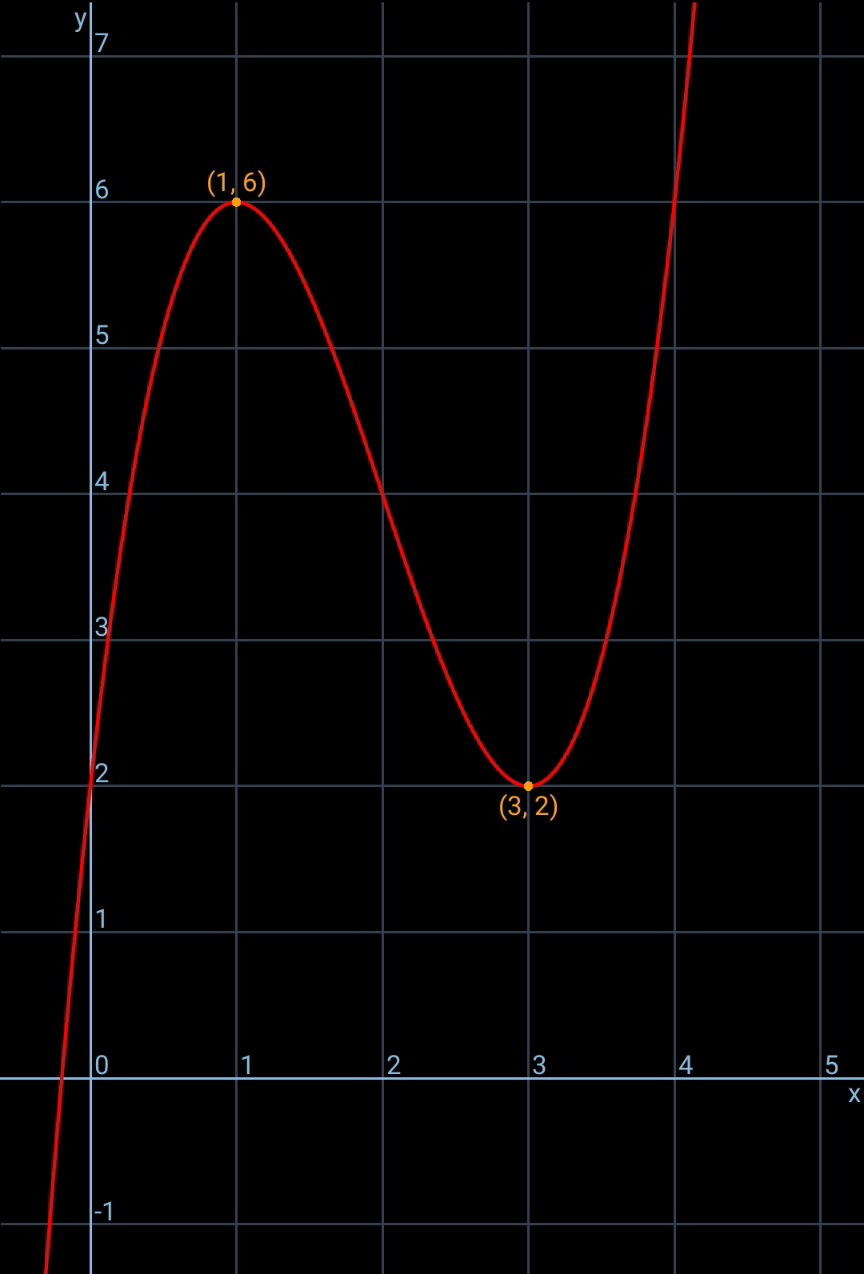
Commented by liberty last updated on 16/Nov/20
$$\mathrm{yes}...\mathrm{thanks}... \\ $$
Commented by benjo_mathlover last updated on 17/Nov/20
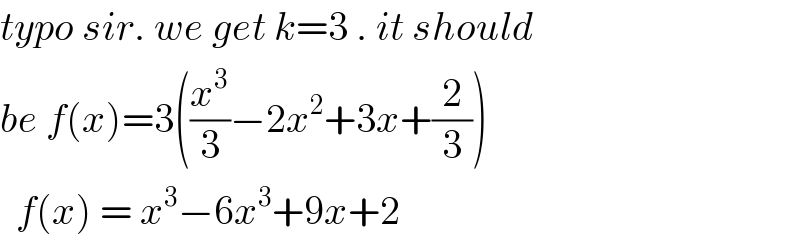
$${typo}\:{sir}.\:{we}\:{get}\:{k}=\mathrm{3}\:.\:{it}\:{should} \\ $$$${be}\:{f}\left({x}\right)=\mathrm{3}\left(\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{3}{x}+\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$\:\:{f}\left({x}\right)\:=\:{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{3}} +\mathrm{9}{x}+\mathrm{2} \\ $$
Commented by mr W last updated on 17/Nov/20

$${yes},\:{thanks}! \\ $$
