
Question Number 12209 by tawa last updated on 16/Apr/17
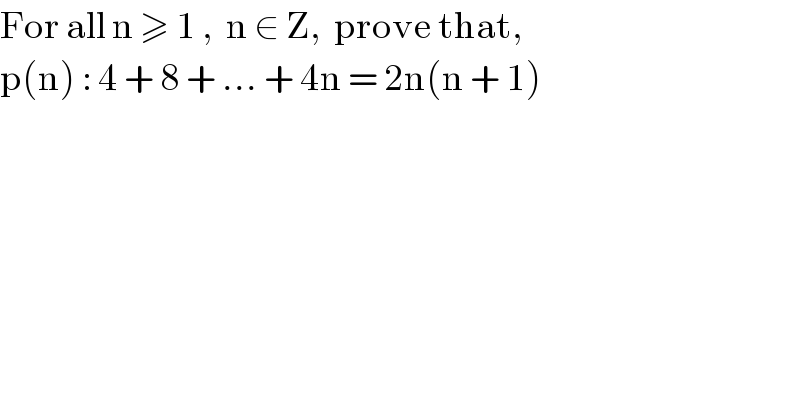
$$\mathrm{For}\:\mathrm{all}\:\mathrm{n}\:\geqslant\:\mathrm{1}\:,\:\:\mathrm{n}\:\in\:\mathrm{Z},\:\:\mathrm{prove}\:\mathrm{that},\: \\ $$$$\mathrm{p}\left(\mathrm{n}\right)\::\:\mathrm{4}\:+\:\mathrm{8}\:+\:...\:+\:\mathrm{4n}\:=\:\mathrm{2n}\left(\mathrm{n}\:+\:\mathrm{1}\right) \\ $$
Commented by tawa last updated on 16/Apr/17

$$\mathrm{please}\:\mathrm{show}\:\mathrm{me}\:\mathrm{full}\:\mathrm{workings}\:\mathrm{sirs}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{all}. \\ $$
Answered by mrW1 last updated on 16/Apr/17
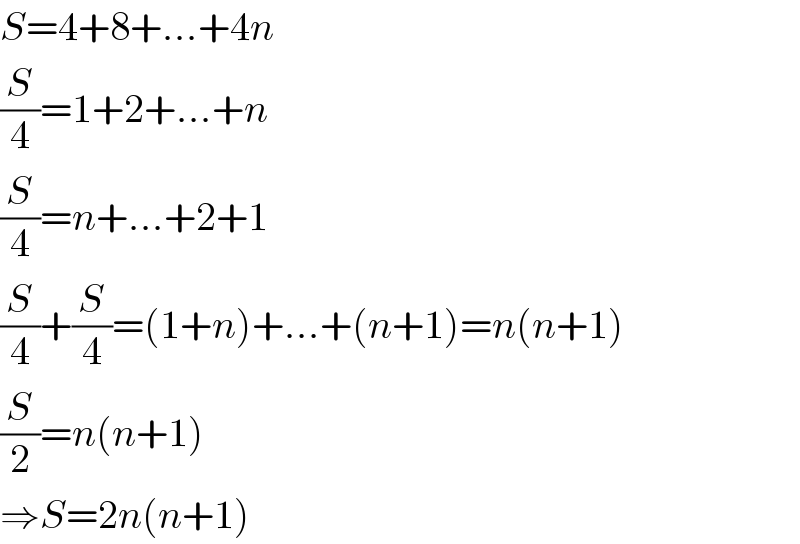
$${S}=\mathrm{4}+\mathrm{8}+...+\mathrm{4}{n} \\ $$$$\frac{{S}}{\mathrm{4}}=\mathrm{1}+\mathrm{2}+...+{n} \\ $$$$\frac{{S}}{\mathrm{4}}={n}+...+\mathrm{2}+\mathrm{1} \\ $$$$\frac{{S}}{\mathrm{4}}+\frac{{S}}{\mathrm{4}}=\left(\mathrm{1}+{n}\right)+...+\left({n}+\mathrm{1}\right)={n}\left({n}+\mathrm{1}\right) \\ $$$$\frac{{S}}{\mathrm{2}}={n}\left({n}+\mathrm{1}\right) \\ $$$$\Rightarrow{S}=\mathrm{2}{n}\left({n}+\mathrm{1}\right) \\ $$
Commented by tawa last updated on 16/Apr/17

$$\mathrm{i}\:\mathrm{appreciate}\:\mathrm{sir}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}. \\ $$
