
Question Number 122053 by 676597498 last updated on 13/Nov/20
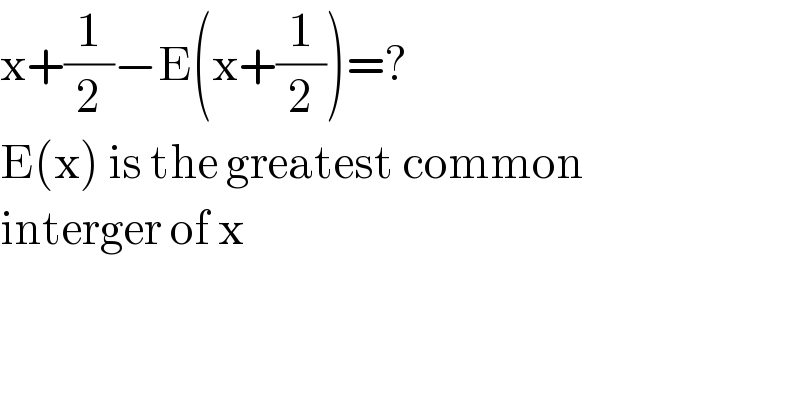
$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{E}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=? \\ $$$$\mathrm{E}\left(\mathrm{x}\right)\:\mathrm{is}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{common} \\ $$$$\mathrm{interger}\:\mathrm{of}\:\mathrm{x} \\ $$
Commented by mr W last updated on 13/Nov/20
![x−[x]={x} ⇒ x+(1/2)−E(x+(1/2))={x+(1/2)}](Q122061.png)
$${x}−\left[{x}\right]=\left\{{x}\right\} \\ $$$$\Rightarrow\:\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{E}\left(\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right)=\left\{{x}+\frac{\mathrm{1}}{\mathrm{2}}\right\} \\ $$
Commented by 676597498 last updated on 13/Nov/20
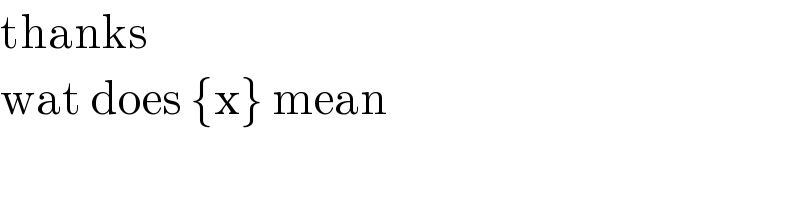
$$\mathrm{thanks} \\ $$$$\mathrm{wat}\:\mathrm{does}\:\left\{\mathrm{x}\right\}\:\mathrm{mean} \\ $$
Commented by mr W last updated on 13/Nov/20
![the fractional part of x: {x}=x−[x]](Q122067.png)
$${the}\:{fractional}\:{part}\:{of}\:{x}: \\ $$$$\left\{{x}\right\}={x}−\left[{x}\right] \\ $$
Answered by mathmax by abdo last updated on 15/Nov/20
![x+(1/2)−[x+(1/2)] ={x+(1/2)} (u−[u]={u})](Q122229.png)
$$\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}−\left[\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right]\:=\left\{\mathrm{x}+\frac{\mathrm{1}}{\mathrm{2}}\right\}\:\:\:\left(\mathrm{u}−\left[\mathrm{u}\right]=\left\{\mathrm{u}\right\}\right) \\ $$
