
Question Number 121989 by mlj5 last updated on 13/Nov/20

$${determiner}\:{le}\:{plus}\:{grand}\:{entier}\:{de}\:{n}\:{tel}\:{que} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}+\sqrt{\mathrm{1}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{4}}+\sqrt{\mathrm{3}}}+...\frac{\mathrm{1}}{\:\sqrt{{n}+\mathrm{1}}+\sqrt{{n}}}\leqslant\mathrm{9} \\ $$
Answered by Ar Brandon last updated on 13/Nov/20
![S_n =Σ_(k=1) ^n (1/( (√(k+1))+(√k)))=Σ_(k=1) ^n (((√(k+1))−(√k))/1) =Σ_(k=1) ^n [(√(k+1))−(√k)]=((√2)−(√1))+((√3)−(√2))+∙∙∙ +((√n)−(√(n−1)))+((√(n+1))−(√n)) Par te^� le^� scopage nous avons −(√1)+(√(n+1)) (√(n+1))−1≤9 ⇒ (√(n+1))≤10 ⇒n+1≤100 ⇒ n ≤ 99 D′ou^� le plus grand entier est n=99](Q121990.png)
$$\mathrm{S}_{\mathrm{n}} =\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\:\sqrt{\mathrm{k}+\mathrm{1}}+\sqrt{\mathrm{k}}}=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\sqrt{\mathrm{k}+\mathrm{1}}−\sqrt{\mathrm{k}}}{\mathrm{1}} \\ $$$$\:\:\:\:\:=\underset{\mathrm{k}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left[\sqrt{\mathrm{k}+\mathrm{1}}−\sqrt{\mathrm{k}}\right]=\left(\sqrt{\mathrm{2}}−\sqrt{\mathrm{1}}\right)+\left(\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}\right)+\centerdot\centerdot\centerdot \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\sqrt{\mathrm{n}}−\sqrt{\mathrm{n}−\mathrm{1}}\right)+\left(\sqrt{\mathrm{n}+\mathrm{1}}−\sqrt{\mathrm{n}}\right) \\ $$$$\mathrm{Par}\:\mathrm{t}\acute {\mathrm{e}l}\acute {\mathrm{e}scopage}\:\mathrm{nous}\:\mathrm{avons}\:−\sqrt{\mathrm{1}}+\sqrt{\mathrm{n}+\mathrm{1}} \\ $$$$\sqrt{\mathrm{n}+\mathrm{1}}−\mathrm{1}\leqslant\mathrm{9}\:\Rightarrow\:\sqrt{\mathrm{n}+\mathrm{1}}\leqslant\mathrm{10} \\ $$$$\Rightarrow\mathrm{n}+\mathrm{1}\leqslant\mathrm{100}\:\Rightarrow\:\mathrm{n}\:\leqslant\:\mathrm{99} \\ $$$$\mathrm{D}'\mathrm{o}\grave {\mathrm{u}}\:\mathrm{le}\:\mathrm{plus}\:\mathrm{grand}\:\mathrm{entier}\:\mathrm{est}\:\mathrm{n}=\mathrm{99} \\ $$
Answered by Dwaipayan Shikari last updated on 13/Nov/20
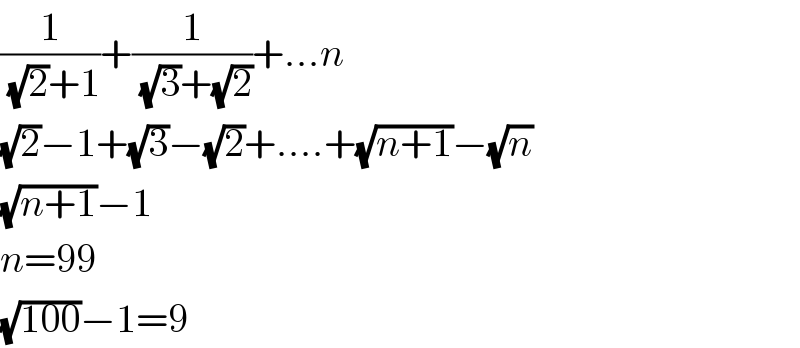
$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}+\mathrm{1}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+\sqrt{\mathrm{2}}}+...{n} \\ $$$$\sqrt{\mathrm{2}}−\mathrm{1}+\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}}+....+\sqrt{{n}+\mathrm{1}}−\sqrt{{n}} \\ $$$$\sqrt{{n}+\mathrm{1}}−\mathrm{1} \\ $$$${n}=\mathrm{99} \\ $$$$\sqrt{\mathrm{100}}−\mathrm{1}=\mathrm{9} \\ $$
