
Question Number 121956 by bemath last updated on 13/Nov/20
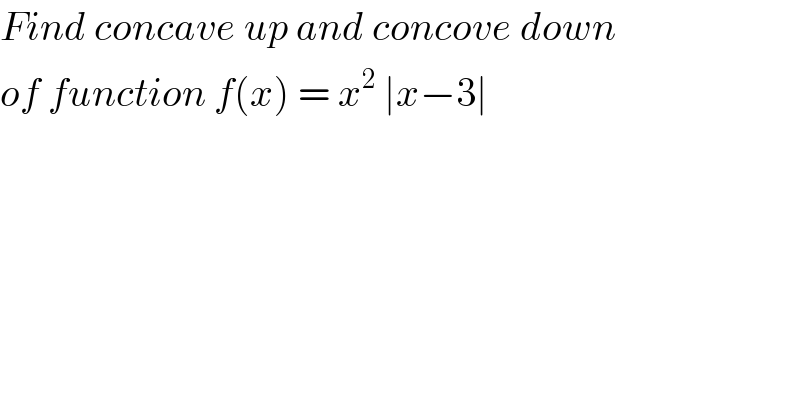
$${Find}\:{concave}\:{up}\:{and}\:{concove}\:{down} \\ $$$${of}\:{function}\:{f}\left({x}\right)\:=\:{x}^{\mathrm{2}} \:\mid{x}−\mathrm{3}\mid\: \\ $$
Answered by MJS_new last updated on 13/Nov/20
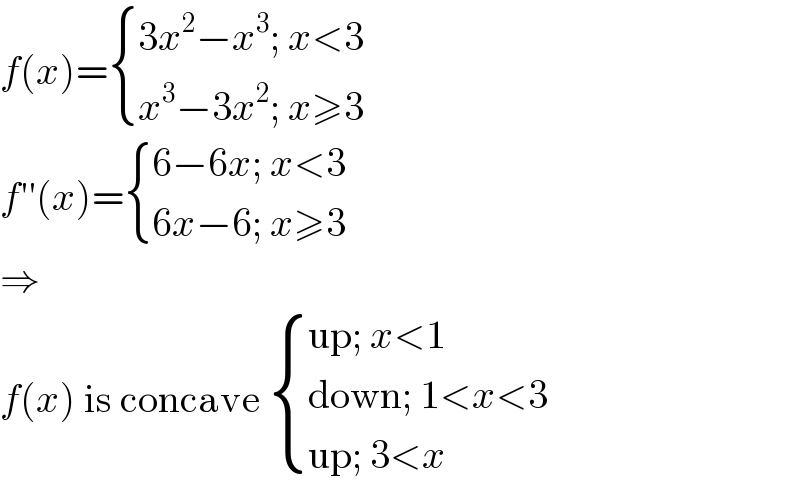
$${f}\left({x}\right)=\begin{cases}{\mathrm{3}{x}^{\mathrm{2}} −{x}^{\mathrm{3}} ;\:{x}<\mathrm{3}}\\{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} ;\:{x}\geqslant\mathrm{3}}\end{cases} \\ $$$${f}''\left({x}\right)=\begin{cases}{\mathrm{6}−\mathrm{6}{x};\:{x}<\mathrm{3}}\\{\mathrm{6}{x}−\mathrm{6};\:{x}\geqslant\mathrm{3}}\end{cases} \\ $$$$\Rightarrow \\ $$$${f}\left({x}\right)\:\mathrm{is}\:\mathrm{concave}\:\begin{cases}{\mathrm{up};\:{x}<\mathrm{1}}\\{\mathrm{down};\:\mathrm{1}<{x}<\mathrm{3}}\\{\mathrm{up};\:\mathrm{3}<{x}}\end{cases} \\ $$
