Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 121875 by rs4089 last updated on 12/Nov/20

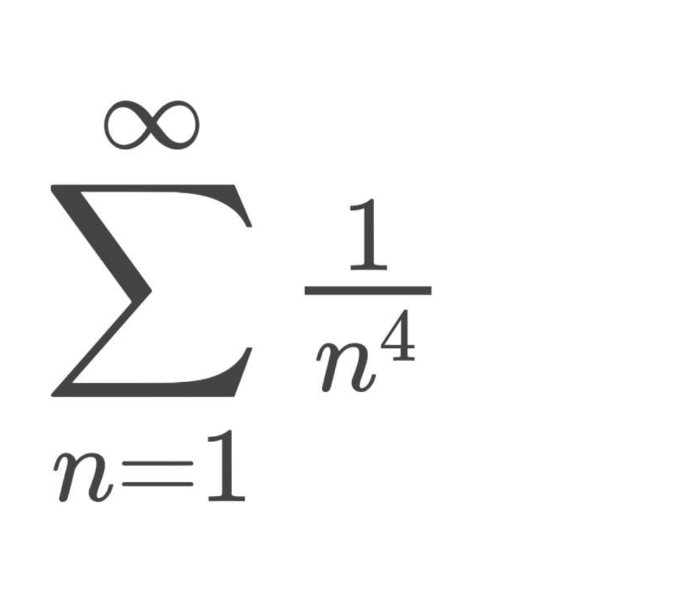
Answered by Dwaipayan Shikari last updated on 12/Nov/20

(π^4 /(90))

$$\frac{\pi^{\mathrm{4}} }{\mathrm{90}} \\ $$

Answered by Dwaipayan Shikari last updated on 12/Nov/20

((sinπx)/(πx))=Π_(n=1) ^∞ (1−(x^2 /n^2 )) ((sinu)/u)=Π_(n=1) ^∞ (1−(u^2 /(π^2 n^2 ))) 1−(u^2 /6)+(u^4 /(120))−...=(1−(u^2 /π^2 ))(1−(u^2 /(4π^2 )))(1−(u^2 /(9π^2 )))(1−(u^2 /(16π^2 )))... 1−(u^2 /6)+(u^4 /(120))−...=1−((u^2 /π^2 )+(u^2 /(4π^2 ))+...)+(3/4)((u^4 /π^4 )+(u^4 /(16π^4 ))+...)+.... (u^2 /6)=u^2 ((1/π^2 )+(1/(4π^2 ))+...) 1+(1/4)+(1/9)+..=(π^2 /6) (u^4 /(120))=(3/4)((u^4 /π^4 )+(u^4 /(16π^4 ))+.....) 1+(1/(16))+(1/(81))+...=(π^4 /(90))

$$\frac{{sin}\pi{x}}{\pi{x}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right) \\ $$$$\frac{{sinu}}{{u}}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\prod}}\left(\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\pi^{\mathrm{2}} {n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{6}}+\frac{{u}^{\mathrm{4}} }{\mathrm{120}}−...=\left(\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\pi^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{4}\pi^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{9}\pi^{\mathrm{2}} }\right)\left(\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{16}\pi^{\mathrm{2}} }\right)... \\ $$$$\mathrm{1}−\frac{{u}^{\mathrm{2}} }{\mathrm{6}}+\frac{{u}^{\mathrm{4}} }{\mathrm{120}}−...=\mathrm{1}−\left(\frac{{u}^{\mathrm{2}} }{\pi^{\mathrm{2}} }+\frac{{u}^{\mathrm{2}} }{\mathrm{4}\pi^{\mathrm{2}} }+...\right)+\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{{u}^{\mathrm{4}} }{\pi^{\mathrm{4}} }+\frac{{u}^{\mathrm{4}} }{\mathrm{16}\pi^{\mathrm{4}} }+...\right)+.... \\ $$$$\frac{{u}^{\mathrm{2}} }{\mathrm{6}}={u}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\pi^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}\pi^{\mathrm{2}} }+...\right) \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{9}}+..=\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$\frac{{u}^{\mathrm{4}} }{\mathrm{120}}=\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{{u}^{\mathrm{4}} }{\pi^{\mathrm{4}} }+\frac{{u}^{\mathrm{4}} }{\mathrm{16}\pi^{\mathrm{4}} }+.....\right) \\ $$$$\mathrm{1}+\frac{\mathrm{1}}{\mathrm{16}}+\frac{\mathrm{1}}{\mathrm{81}}+...=\frac{\pi^{\mathrm{4}} }{\mathrm{90}} \\ $$

Commented by mnjuly1970 last updated on 12/Nov/20

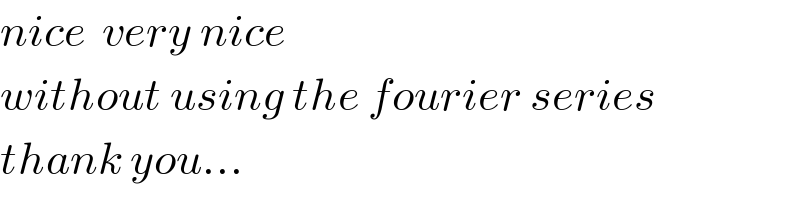
nice very nice without using the fourier series thank you...

$${nice}\:\:{very}\:{nice}\: \\ $$$${without}\:{using}\:{the}\:{fourier}\:{series}\: \\ $$$${thank}\:{you}... \\ $$

Commented by Dwaipayan Shikari last updated on 12/Nov/20

�� with pleasure sir!

Terms of Service

Privacy Policy

Contact: info@tinkutara.com