
Question Number 121869 by mnjuly1970 last updated on 12/Nov/20
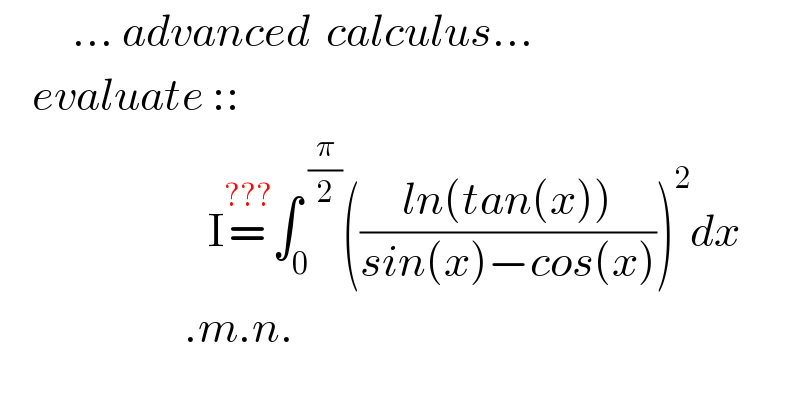
$$\:\:\:\:\:\:\:\:\:...\:{advanced}\:\:{calculus}... \\ $$$$\:\:\:\:{evaluate}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{I}\overset{???} {=}\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{2}}} \left(\frac{{ln}\left({tan}\left({x}\right)\right)}{{sin}\left({x}\right)−{cos}\left({x}\right)}\right)^{\mathrm{2}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.{m}.{n}. \\ $$
Answered by mindispower last updated on 12/Nov/20
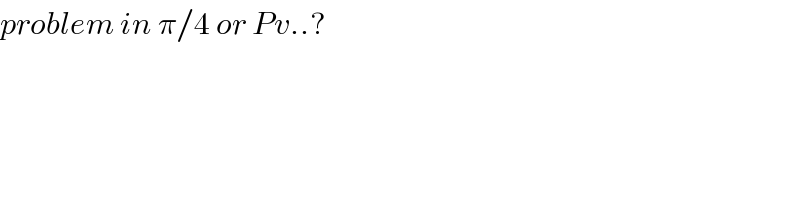
$${problem}\:{in}\:\pi/\mathrm{4}\:{or}\:{Pv}..? \\ $$
Commented by mnjuly1970 last updated on 13/Nov/20
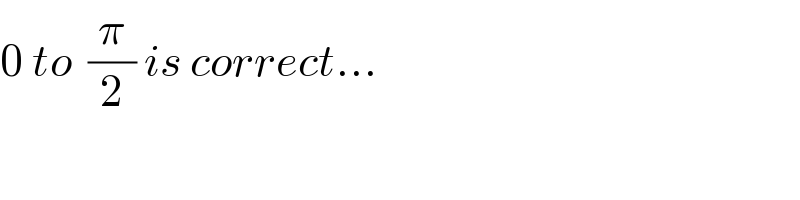
$$\mathrm{0}\:{to}\:\:\frac{\pi}{\mathrm{2}}\:{is}\:{correct}... \\ $$
Answered by mindispower last updated on 13/Nov/20
![(sin(x)−cos(x))^2 =(((tg(x)−1)^2 )/(1+tg^2 (x))) I=∫_0 ^(π/2) ((ln^2 (tg(x)))/((tg(x)−1)^2 ))dtg(x) tg(x)=t⇒I=∫_0 ^∞ ((ln^2 (r))/((r−1)^2 ))dr =∫_0 ^1 (((ln^2 (r))/((r−1)^2 )).dr+((ln^2 ((1/r)))/(((1/r)−1)^2 )).(dr/r^2 )) ∫_0 ^1 ((ln^2 (r)dr)/((r−1)^2 ))..IBP⇒ lim_(t→0) [((−ln^2 (r))/(r−1))]_t ^1 +2∫_t ^1 ((ln(r))/(r(r−1)))dr =lim_(t→0) ((ln^2 (t))/(t−1))+2∫_t ^1 ((ln(r))/(r−1))dr−2∫_t ^1 ((ln(r))/r)dr =lim_(t→0) ((ln^2 (t))/(t−1))−2∫_0 ^(1−t) ((ln(1−r))/r)dr+ln^2 (t) =lim_(t→0) [(((ln^2 (t))/(t−1))+ln^2 (t))+2Li_2 (1−t)] =lim_(t→0) [((tln^2 (t))/(t−1))]+2Li_2 (1) cause Li_2 is continus =2Li_2 (1)=2.(π^2 /6)=(π^2 /3)](Q121976.png)
$$\left({sin}\left({x}\right)−{cos}\left({x}\right)\right)^{\mathrm{2}} =\frac{\left({tg}\left({x}\right)−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{1}+{tg}^{\mathrm{2}} \left({x}\right)} \\ $$$${I}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{ln}^{\mathrm{2}} \left({tg}\left({x}\right)\right)}{\left({tg}\left({x}\right)−\mathrm{1}\right)^{\mathrm{2}} }{dtg}\left({x}\right) \\ $$$${tg}\left({x}\right)={t}\Rightarrow{I}=\int_{\mathrm{0}} ^{\infty} \frac{{ln}^{\mathrm{2}} \left({r}\right)}{\left({r}−\mathrm{1}\right)^{\mathrm{2}} }{dr} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{{ln}^{\mathrm{2}} \left({r}\right)}{\left({r}−\mathrm{1}\right)^{\mathrm{2}} }.{dr}+\frac{{ln}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{r}}\right)}{\left(\frac{\mathrm{1}}{{r}}−\mathrm{1}\right)^{\mathrm{2}} }.\frac{{dr}}{{r}^{\mathrm{2}} }\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({r}\right){dr}}{\left({r}−\mathrm{1}\right)^{\mathrm{2}} }..{IBP}\Rightarrow \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{−{ln}^{\mathrm{2}} \left({r}\right)}{{r}−\mathrm{1}}\right]_{{t}} ^{\mathrm{1}} +\mathrm{2}\int_{{t}} ^{\mathrm{1}} \frac{{ln}\left({r}\right)}{{r}\left({r}−\mathrm{1}\right)}{dr} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ln}^{\mathrm{2}} \left({t}\right)}{{t}−\mathrm{1}}+\mathrm{2}\int_{{t}} ^{\mathrm{1}} \frac{{ln}\left({r}\right)}{{r}−\mathrm{1}}{dr}−\mathrm{2}\int_{{t}} ^{\mathrm{1}} \frac{{ln}\left({r}\right)}{{r}}{dr} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{ln}^{\mathrm{2}} \left({t}\right)}{{t}−\mathrm{1}}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}−{t}} \frac{{ln}\left(\mathrm{1}−{r}\right)}{{r}}{dr}+{ln}^{\mathrm{2}} \left({t}\right)\: \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\frac{{ln}^{\mathrm{2}} \left({t}\right)}{{t}−\mathrm{1}}+{ln}^{\mathrm{2}} \left({t}\right)\right)+\mathrm{2}{Li}_{\mathrm{2}} \left(\mathrm{1}−{t}\right)\right] \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\frac{{tln}^{\mathrm{2}} \left({t}\right)}{{t}−\mathrm{1}}\right]+\mathrm{2}{Li}_{\mathrm{2}} \left(\mathrm{1}\right)\:\:{cause}\:{Li}_{\mathrm{2}} {is}\:{continus} \\ $$$$=\mathrm{2}{Li}_{\mathrm{2}} \left(\mathrm{1}\right)=\mathrm{2}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=\frac{\pi^{\mathrm{2}} }{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 13/Nov/20

$${bravo}\:{bravo} \\ $$$${sir}\:\:{mindspower} \\ $$$$\:{thank}\:{you}\:{so}\:{much}... \\ $$
Commented by mindispower last updated on 13/Nov/20
$${thanx}\:{always}\:{a}\:{pleasur} \\ $$
