
Question Number 121848 by danielasebhofoh last updated on 12/Nov/20

Answered by TANMAY PANACEA last updated on 12/Nov/20
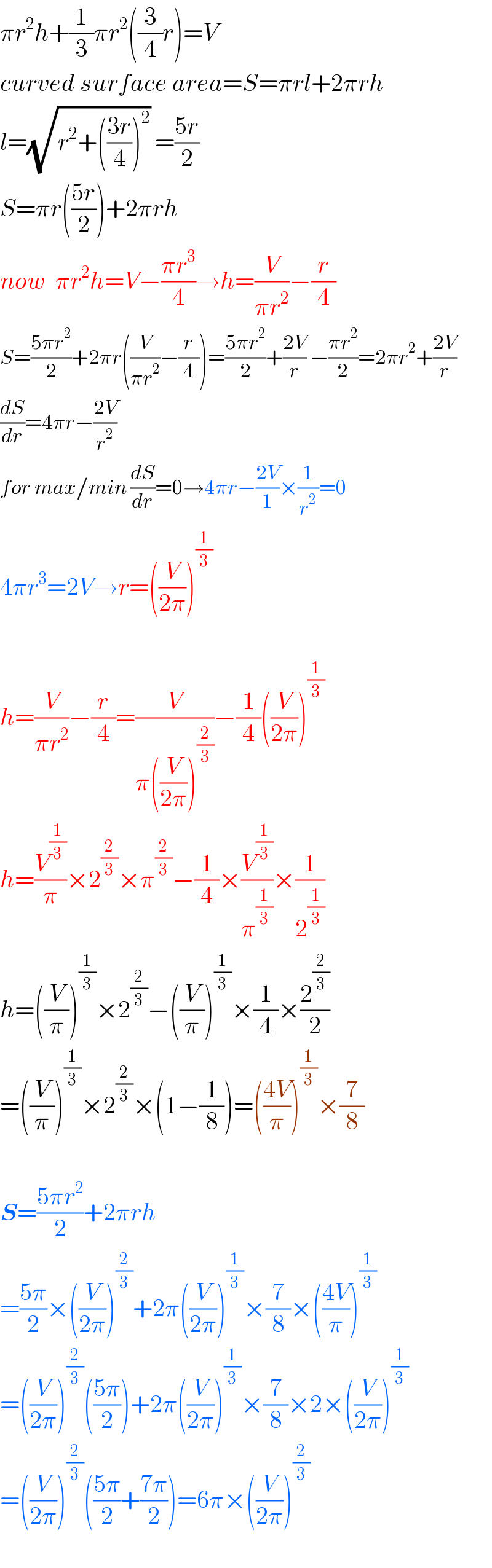
$$\pi{r}^{\mathrm{2}} {h}+\frac{\mathrm{1}}{\mathrm{3}}\pi{r}^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}{r}\right)={V} \\ $$$${curved}\:{surface}\:{area}={S}=\pi{rl}+\mathrm{2}\pi{rh} \\ $$$${l}=\sqrt{{r}^{\mathrm{2}} +\left(\frac{\mathrm{3}{r}}{\mathrm{4}}\right)^{\mathrm{2}} }\:=\frac{\mathrm{5}{r}}{\mathrm{2}} \\ $$$${S}=\pi{r}\left(\frac{\mathrm{5}{r}}{\mathrm{2}}\right)+\mathrm{2}\pi{rh} \\ $$$${now}\:\:\pi{r}^{\mathrm{2}} {h}={V}−\frac{\pi{r}^{\mathrm{3}} }{\mathrm{4}}\rightarrow{h}=\frac{{V}}{\pi{r}^{\mathrm{2}} }−\frac{{r}}{\mathrm{4}} \\ $$$${S}=\frac{\mathrm{5}\pi{r}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\pi{r}\left(\frac{{V}}{\pi{r}^{\mathrm{2}} }−\frac{{r}}{\mathrm{4}}\right)=\frac{\mathrm{5}\pi{r}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{2}{V}}{{r}}\:−\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{2}\pi{r}^{\mathrm{2}} +\frac{\mathrm{2}{V}}{{r}} \\ $$$$\frac{{dS}}{{dr}}=\mathrm{4}\pi{r}−\frac{\mathrm{2}{V}}{{r}^{\mathrm{2}} } \\ $$$${for}\:{max}/{min}\:\frac{{dS}}{{dr}}=\mathrm{0}\rightarrow\mathrm{4}\pi{r}−\frac{\mathrm{2}{V}}{\mathrm{1}}×\frac{\mathrm{1}}{{r}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\mathrm{4}\pi{r}^{\mathrm{3}} =\mathrm{2}{V}\rightarrow{r}=\left(\frac{{V}}{\mathrm{2}\pi}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$ \\ $$$${h}=\frac{{V}}{\pi{r}^{\mathrm{2}} }−\frac{{r}}{\mathrm{4}}=\frac{{V}}{\pi\left(\frac{{V}}{\mathrm{2}\pi}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} }−\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{{V}}{\mathrm{2}\pi}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$${h}=\frac{{V}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\pi}×\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} ×\pi^{\frac{\mathrm{2}}{\mathrm{3}}} −\frac{\mathrm{1}}{\mathrm{4}}×\frac{{V}^{\frac{\mathrm{1}}{\mathrm{3}}} }{\pi^{\frac{\mathrm{1}}{\mathrm{3}}} }×\frac{\mathrm{1}}{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$${h}=\left(\frac{{V}}{\pi}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ×\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} −\left(\frac{{V}}{\pi}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ×\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} }{\mathrm{2}} \\ $$$$=\left(\frac{{V}}{\pi}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ×\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} ×\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{8}}\right)=\left(\frac{\mathrm{4}{V}}{\pi}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ×\frac{\mathrm{7}}{\mathrm{8}} \\ $$$$ \\ $$$$\boldsymbol{{S}}=\frac{\mathrm{5}\pi{r}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\pi{rh} \\ $$$$=\frac{\mathrm{5}\pi}{\mathrm{2}}×\left(\frac{{V}}{\mathrm{2}\pi}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{2}\pi\left(\frac{{V}}{\mathrm{2}\pi}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ×\frac{\mathrm{7}}{\mathrm{8}}×\left(\frac{\mathrm{4}{V}}{\pi}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\left(\frac{{V}}{\mathrm{2}\pi}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\frac{\mathrm{5}\pi}{\mathrm{2}}\right)+\mathrm{2}\pi\left(\frac{{V}}{\mathrm{2}\pi}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} ×\frac{\mathrm{7}}{\mathrm{8}}×\mathrm{2}×\left(\frac{{V}}{\mathrm{2}\pi}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\left(\frac{{V}}{\mathrm{2}\pi}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\frac{\mathrm{5}\pi}{\mathrm{2}}+\frac{\mathrm{7}\pi}{\mathrm{2}}\right)=\mathrm{6}\pi×\left(\frac{{V}}{\mathrm{2}\pi}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$ \\ $$
