
Question Number 121697 by Vishal Sharma last updated on 11/Nov/20

$$\:\mathbb{Q}.\:\mathbb{FACTORIZE}− \\ $$$$\:\left(\mathrm{1}\right)\:\mathrm{9x}^{\mathrm{2}} +\mathrm{12xy}+\mathrm{4y}^{\mathrm{2}} \\ $$$$\:\left(\mathrm{2}\right)\:\mathrm{25x}^{\mathrm{2}} −\mathrm{20xy}+\mathrm{16y}^{\mathrm{2}} \\ $$$$\:\left(\mathrm{3}\right)\:\mathrm{36x}^{\mathrm{2}} +\mathrm{42xy}+\mathrm{49y}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\bigstar\bigstar\mathbb{VISHAL}\bigstar\bigstar \\ $$
Answered by bemath last updated on 11/Nov/20
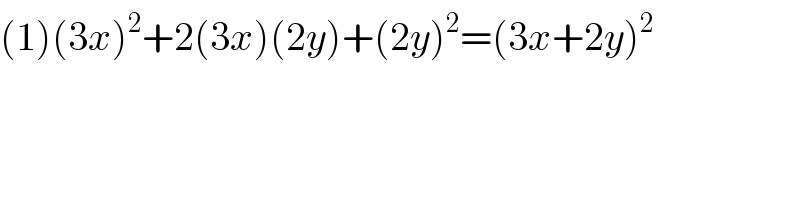
$$\left(\mathrm{1}\right)\left(\mathrm{3}{x}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{3}{x}\right)\left(\mathrm{2}{y}\right)+\left(\mathrm{2}{y}\right)^{\mathrm{2}} =\left(\mathrm{3}{x}+\mathrm{2}{y}\right)^{\mathrm{2}} \\ $$
Answered by TANMAY PANACEA last updated on 11/Nov/20
![2)(5x)^2 −5x×4y+(4y)^2 (5x)^2 −5x×4y+(4y)^2 a^2 −ab+b^2 a^2 +(w+w^2 )ab+b^2 a^2 +abw+abw^2 +b^2 a(a+bw)+bw^2 (a+bw) (a+bw)(a+bw^2 ) [1+w+w^2 =0 w^3 =1] (5x+w4y)(5x+w^2 4y)](Q121699.png)
$$\left.\mathrm{2}\right)\left(\mathrm{5}{x}\right)^{\mathrm{2}} −\mathrm{5}{x}×\mathrm{4}{y}+\left(\mathrm{4}{y}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{5}{x}\right)^{\mathrm{2}} −\mathrm{5}{x}×\mathrm{4}{y}+\left(\mathrm{4}{y}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +\left({w}+{w}^{\mathrm{2}} \right){ab}+{b}^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{abw}+{abw}^{\mathrm{2}} +{b}^{\mathrm{2}} \\ $$$${a}\left({a}+{bw}\right)+{bw}^{\mathrm{2}} \left({a}+{bw}\right) \\ $$$$\left({a}+{bw}\right)\left({a}+{bw}^{\mathrm{2}} \right)\:\:\:\left[\mathrm{1}+{w}+{w}^{\mathrm{2}} =\mathrm{0}\:\:{w}^{\mathrm{3}} =\mathrm{1}\right] \\ $$$$\left(\mathrm{5}{x}+{w}\mathrm{4}{y}\right)\left(\mathrm{5}{x}+{w}^{\mathrm{2}} \mathrm{4}{y}\right) \\ $$
Answered by TANMAY PANACEA last updated on 11/Nov/20
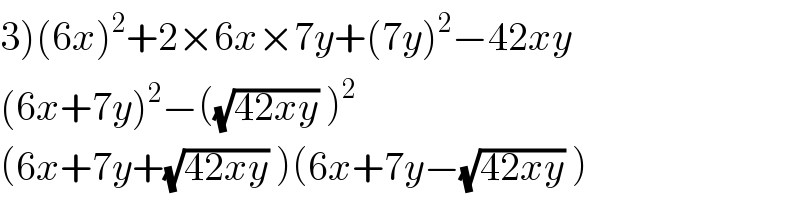
$$\left.\mathrm{3}\right)\left(\mathrm{6}{x}\right)^{\mathrm{2}} +\mathrm{2}×\mathrm{6}{x}×\mathrm{7}{y}+\left(\mathrm{7}{y}\right)^{\mathrm{2}} −\mathrm{42}{xy} \\ $$$$\left(\mathrm{6}{x}+\mathrm{7}{y}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{42}{xy}}\:\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{6}{x}+\mathrm{7}{y}+\sqrt{\mathrm{42}{xy}}\:\right)\left(\mathrm{6}{x}+\mathrm{7}{y}−\sqrt{\mathrm{42}{xy}}\:\right) \\ $$
