
Previous in Differential Equation Next in Differential Equation
Question Number 121633 by liberty last updated on 10/Nov/20
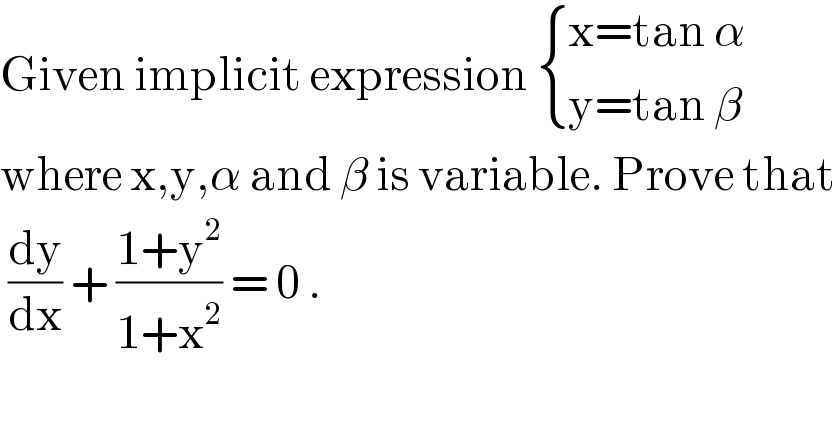
$$\mathrm{Given}\:\mathrm{implicit}\:\mathrm{expression}\:\begin{cases}{\mathrm{x}=\mathrm{tan}\:\alpha}\\{\mathrm{y}=\mathrm{tan}\:\beta}\end{cases} \\ $$$$\mathrm{where}\:\mathrm{x},\mathrm{y},\alpha\:\mathrm{and}\:\beta\:\mathrm{is}\:\mathrm{variable}.\:\mathrm{Prove}\:\mathrm{that} \\ $$$$\:\frac{\mathrm{dy}}{\mathrm{dx}}\:+\:\frac{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{0}\:. \\ $$
Commented by Dwaipayan Shikari last updated on 10/Nov/20
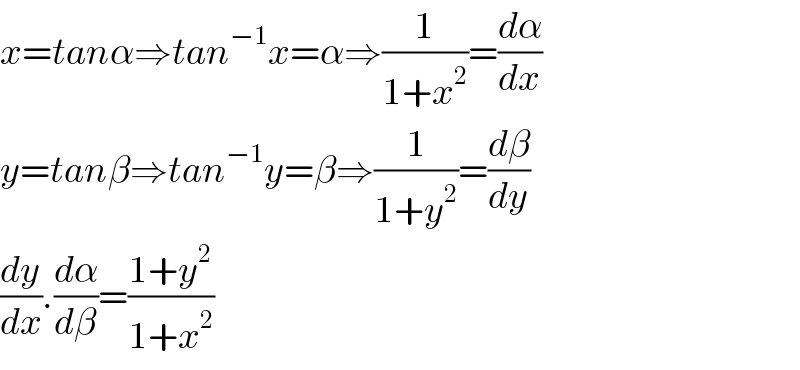
$${x}={tan}\alpha\Rightarrow{tan}^{−\mathrm{1}} {x}=\alpha\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }=\frac{{d}\alpha}{{dx}} \\ $$$${y}={tan}\beta\Rightarrow{tan}^{−\mathrm{1}} {y}=\beta\Rightarrow\frac{\mathrm{1}}{\mathrm{1}+{y}^{\mathrm{2}} }=\frac{{d}\beta}{{dy}} \\ $$$$\frac{{dy}}{{dx}}.\frac{{d}\alpha}{{d}\beta}=\frac{\mathrm{1}+{y}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$
Commented by liberty last updated on 10/Nov/20

$$\mathrm{not}\:\mathrm{proved}? \\ $$
Commented by Dwaipayan Shikari last updated on 10/Nov/20
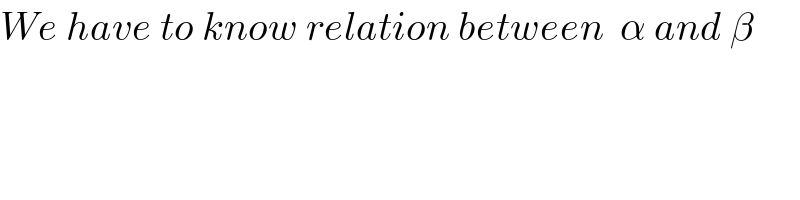
$${We}\:{have}\:{to}\:{know}\:{relation}\:{between}\:\:\alpha\:{and}\:\beta \\ $$
Commented by Dwaipayan Shikari last updated on 10/Nov/20
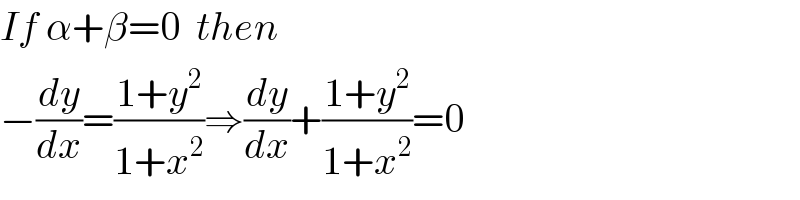
$${If}\:\alpha+\beta=\mathrm{0}\:\:{then} \\ $$$$−\frac{{dy}}{{dx}}=\frac{\mathrm{1}+{y}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\Rightarrow\frac{{dy}}{{dx}}+\frac{\mathrm{1}+{y}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }=\mathrm{0} \\ $$
