
Question Number 121618 by SOMEDAVONG last updated on 10/Nov/20
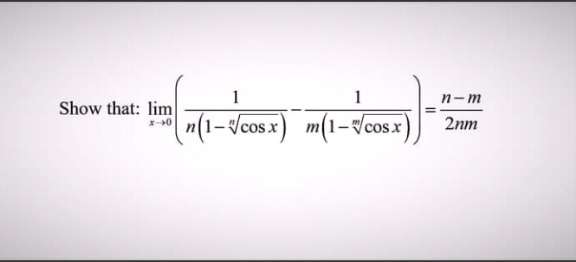
Answered by bemath last updated on 10/Nov/20
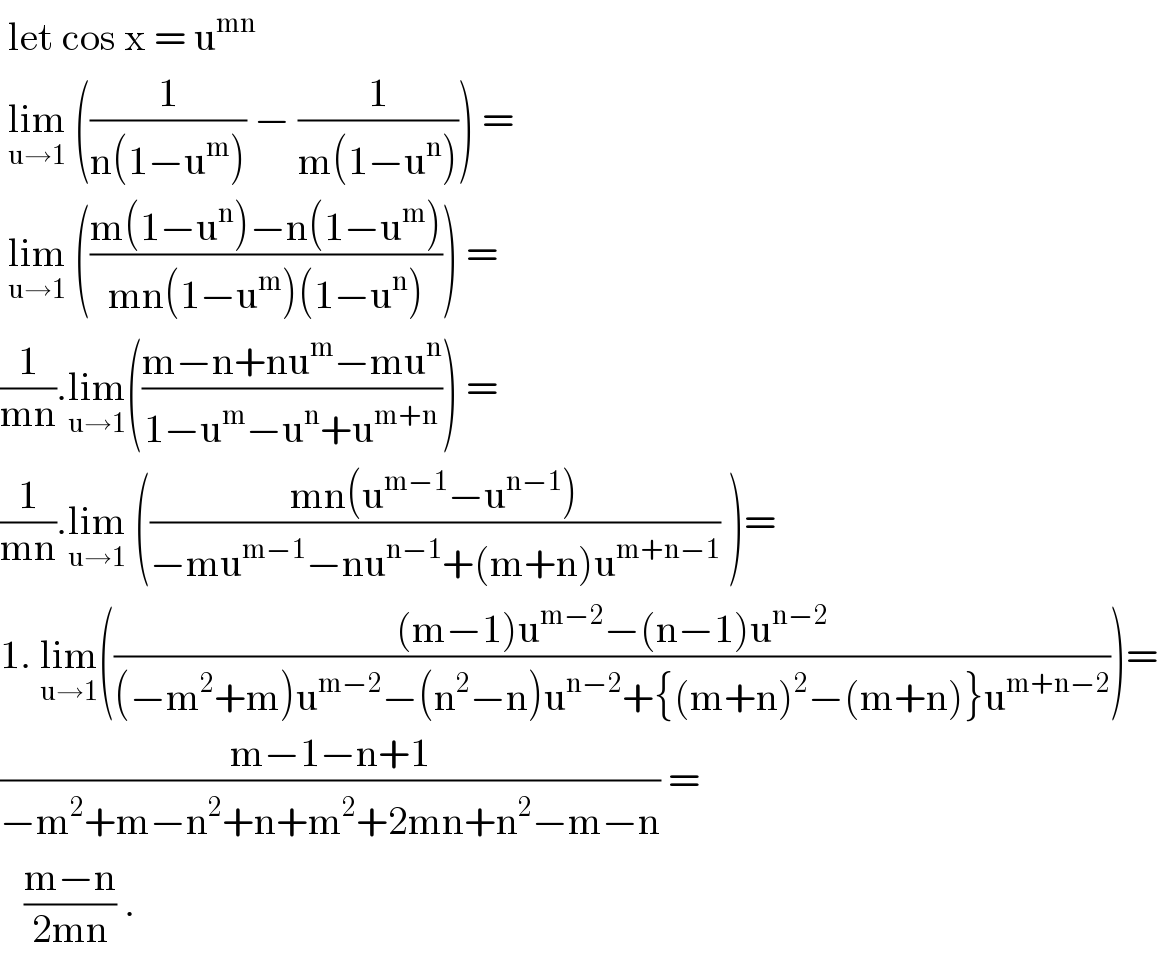
$$\:\mathrm{let}\:\mathrm{cos}\:\mathrm{x}\:=\:\mathrm{u}^{\mathrm{mn}\:} \\ $$$$\:\underset{\mathrm{u}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{1}−\mathrm{u}^{\mathrm{m}} \right)}\:−\:\frac{\mathrm{1}}{\mathrm{m}\left(\mathrm{1}−\mathrm{u}^{\mathrm{n}} \right)}\right)\:= \\ $$$$\:\underset{\mathrm{u}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{m}\left(\mathrm{1}−\mathrm{u}^{\mathrm{n}} \right)−\mathrm{n}\left(\mathrm{1}−\mathrm{u}^{\mathrm{m}} \right)}{\mathrm{mn}\left(\mathrm{1}−\mathrm{u}^{\mathrm{m}} \right)\left(\mathrm{1}−\mathrm{u}^{\mathrm{n}} \right)}\right)\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{mn}}.\underset{\mathrm{u}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\mathrm{m}−\mathrm{n}+\mathrm{nu}^{\mathrm{m}} −\mathrm{mu}^{\mathrm{n}} }{\mathrm{1}−\mathrm{u}^{\mathrm{m}} −\mathrm{u}^{\mathrm{n}} +\mathrm{u}^{\mathrm{m}+\mathrm{n}} }\right)\:= \\ $$$$\frac{\mathrm{1}}{\mathrm{mn}}.\underset{\mathrm{u}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\left(\frac{\mathrm{mn}\left(\mathrm{u}^{\mathrm{m}−\mathrm{1}} −\mathrm{u}^{\mathrm{n}−\mathrm{1}} \right)}{−\mathrm{mu}^{\mathrm{m}−\mathrm{1}} −\mathrm{nu}^{\mathrm{n}−\mathrm{1}} +\left(\mathrm{m}+\mathrm{n}\right)\mathrm{u}^{\mathrm{m}+\mathrm{n}−\mathrm{1}} }\:\right)= \\ $$$$\mathrm{1}.\:\underset{\mathrm{u}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\frac{\left(\mathrm{m}−\mathrm{1}\right)\mathrm{u}^{\mathrm{m}−\mathrm{2}} −\left(\mathrm{n}−\mathrm{1}\right)\mathrm{u}^{\mathrm{n}−\mathrm{2}} }{\left(−\mathrm{m}^{\mathrm{2}} +\mathrm{m}\right)\mathrm{u}^{\mathrm{m}−\mathrm{2}} −\left(\mathrm{n}^{\mathrm{2}} −\mathrm{n}\right)\mathrm{u}^{\mathrm{n}−\mathrm{2}} +\left\{\left(\mathrm{m}+\mathrm{n}\right)^{\mathrm{2}} −\left(\mathrm{m}+\mathrm{n}\right)\right\}\mathrm{u}^{\mathrm{m}+\mathrm{n}−\mathrm{2}} }\right)= \\ $$$$\frac{\mathrm{m}−\mathrm{1}−\mathrm{n}+\mathrm{1}}{−\mathrm{m}^{\mathrm{2}} +\mathrm{m}−\mathrm{n}^{\mathrm{2}} +\mathrm{n}+\mathrm{m}^{\mathrm{2}} +\mathrm{2mn}+\mathrm{n}^{\mathrm{2}} −\mathrm{m}−\mathrm{n}}\:= \\ $$$$\:\:\:\frac{\mathrm{m}−\mathrm{n}}{\mathrm{2mn}}\:.\: \\ $$
Answered by TANMAY PANACEA last updated on 10/Nov/20
![t^(mn) =cosx x→0 cosx→1 t→1 lim_(t→1) (1/(n(1−t^m )))−(1/(m(1−t^n ))) lim_(t→1) ((m−mt^n −n+nt^m )/(mn(1−t^m −t^n +t^(m+n) ))) [using Lhospitsl] (1/(mn))lim_(t→1) ((mn(t^(m−1) −t^(n−1) ))/({0−mt^(m−1) −nt^(n−1) +(m+n)t^(m+n−1) })) =lim_(t→1) (((m−1)t^(m−2) −(n−1)t^(n−2) )/(−m(m−1)t^(m−2) −n(n−1)t^(n−2) +(m+n)(m+n−1)t^(m+n−2) )) =((m−1−n+1)/(−m^2 +m−n^2 +n+m^2 +n^2 +2mn−m−n)) =((m−n)/(2mn))](Q121632.png)
$${t}^{{mn}} ={cosx}\:\:\:{x}\rightarrow\mathrm{0}\:\:{cosx}\rightarrow\mathrm{1}\:\:{t}\rightarrow\mathrm{1} \\ $$$$\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\mathrm{1}}{{n}\left(\mathrm{1}−{t}^{{m}} \right)}−\frac{\mathrm{1}}{{m}\left(\mathrm{1}−{t}^{{n}} \right)} \\ $$$$\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{m}−{mt}^{{n}} −{n}+{nt}^{{m}} }{{mn}\left(\mathrm{1}−{t}^{{m}} −{t}^{{n}} +{t}^{{m}+{n}} \right)}\:\left[{using}\:{Lhospitsl}\right] \\ $$$$\frac{\mathrm{1}}{{mn}}\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{{mn}\left({t}^{{m}−\mathrm{1}} −{t}^{{n}−\mathrm{1}} \right)}{\left\{\mathrm{0}−{mt}^{{m}−\mathrm{1}} −{nt}^{{n}−\mathrm{1}} +\left({m}+{n}\right){t}^{{m}+{n}−\mathrm{1}} \right\}} \\ $$$$=\underset{{t}\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left({m}−\mathrm{1}\right){t}^{{m}−\mathrm{2}} −\left({n}−\mathrm{1}\right){t}^{{n}−\mathrm{2}} }{−{m}\left({m}−\mathrm{1}\right){t}^{{m}−\mathrm{2}} −{n}\left({n}−\mathrm{1}\right){t}^{{n}−\mathrm{2}} +\left({m}+{n}\right)\left({m}+{n}−\mathrm{1}\right){t}^{{m}+{n}−\mathrm{2}} } \\ $$$$=\frac{{m}−\mathrm{1}−{n}+\mathrm{1}}{−{m}^{\mathrm{2}} +{m}−{n}^{\mathrm{2}} +{n}+{m}^{\mathrm{2}} +{n}^{\mathrm{2}} +\mathrm{2}{mn}−{m}−{n}} \\ $$$$=\frac{{m}−{n}}{\mathrm{2}{mn}} \\ $$$$ \\ $$
