
Question Number 121548 by benjo_mathlover last updated on 09/Nov/20
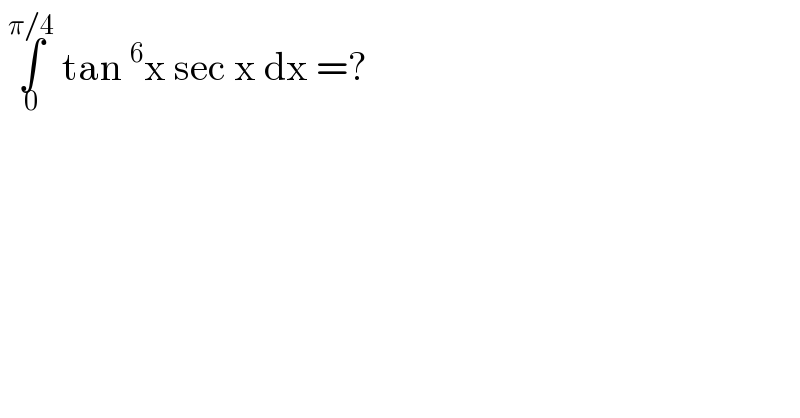
$$\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\:\mathrm{tan}\:^{\mathrm{6}} \mathrm{x}\:\mathrm{sec}\:\mathrm{x}\:\mathrm{dx}\:=? \\ $$
Answered by MJS_new last updated on 09/Nov/20
![∫tan^6 x sec x dx=∫((sin^6 x)/(cos^7 x))dx= [t=(1/(sin x)) → dx=−((sin^2 x)/(cos x))] =−∫(dt/((t^2 −1)^4 ))= [Ostrogradski′s Method] =((t(15t^4 −40t^2 +33))/(48(t^2 −1)^3 ))+(5/(16))∫(dt/(t^2 −1))= =((t(15t^4 −40t^2 +33))/(48(t^2 −1)^3 ))+(5/(32))ln ∣((t−1)/(t+1))∣ the borders are x∈[0; (π/4)] ⇔ t∈]+∞; (√2)] ⇒ answer is −[((t(15t^4 −40t^2 +33))/(48(t^2 −1)^3 ))+(5/(32))ln ∣((t−1)/(t+1))∣]_(√2) ^(+∞) = =((13(√2))/(48))+(5/(16))ln (−1+(√2))](Q121551.png)
$$\int\mathrm{tan}^{\mathrm{6}} \:{x}\:\mathrm{sec}\:{x}\:{dx}=\int\frac{\mathrm{sin}^{\mathrm{6}} \:{x}}{\mathrm{cos}^{\mathrm{7}} \:{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\mathrm{1}}{\mathrm{sin}\:{x}}\:\rightarrow\:{dx}=−\frac{\mathrm{sin}^{\mathrm{2}} \:{x}}{\mathrm{cos}\:{x}}\right] \\ $$$$=−\int\frac{{dt}}{\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{4}} }= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=\frac{{t}\left(\mathrm{15}{t}^{\mathrm{4}} −\mathrm{40}{t}^{\mathrm{2}} +\mathrm{33}\right)}{\mathrm{48}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{16}}\int\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}}= \\ $$$$=\frac{{t}\left(\mathrm{15}{t}^{\mathrm{4}} −\mathrm{40}{t}^{\mathrm{2}} +\mathrm{33}\right)}{\mathrm{48}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{32}}\mathrm{ln}\:\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid \\ $$$$\left.\mathrm{t}\left.\mathrm{he}\:\mathrm{borders}\:\mathrm{are}\:{x}\in\left[\mathrm{0};\:\frac{\pi}{\mathrm{4}}\right]\:\Leftrightarrow\:{t}\in\right]+\infty;\:\sqrt{\mathrm{2}}\right] \\ $$$$\Rightarrow\:\mathrm{answer}\:\mathrm{is} \\ $$$$−\left[\frac{{t}\left(\mathrm{15}{t}^{\mathrm{4}} −\mathrm{40}{t}^{\mathrm{2}} +\mathrm{33}\right)}{\mathrm{48}\left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{32}}\mathrm{ln}\:\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\right]_{\sqrt{\mathrm{2}}} ^{+\infty} = \\ $$$$=\frac{\mathrm{13}\sqrt{\mathrm{2}}}{\mathrm{48}}+\frac{\mathrm{5}}{\mathrm{16}}\mathrm{ln}\:\left(−\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
Commented by liberty last updated on 09/Nov/20

$$\mathrm{waw}...\mathrm{Your}\:\mathrm{method}\:\mathrm{good}\:\mathrm{sir} \\ $$
Commented by Fareed last updated on 09/Nov/20
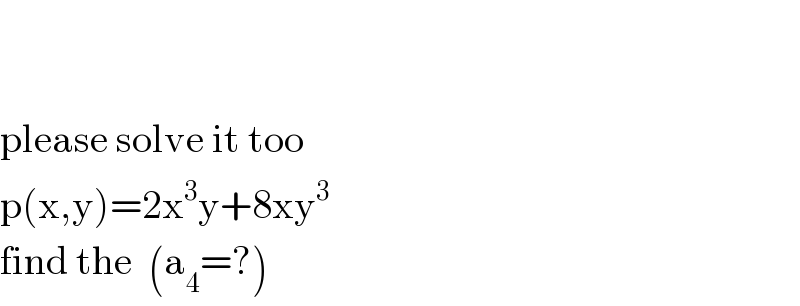
$$ \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{solve}\:\mathrm{it}\:\mathrm{too} \\ $$$$\mathrm{p}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{2x}^{\mathrm{3}} \mathrm{y}+\mathrm{8xy}^{\mathrm{3}} \\ $$$$\mathrm{find}\:\mathrm{the}\:\:\left(\mathrm{a}_{\mathrm{4}} =?\right) \\ $$
