
Question Number 121527 by benjo_mathlover last updated on 09/Nov/20
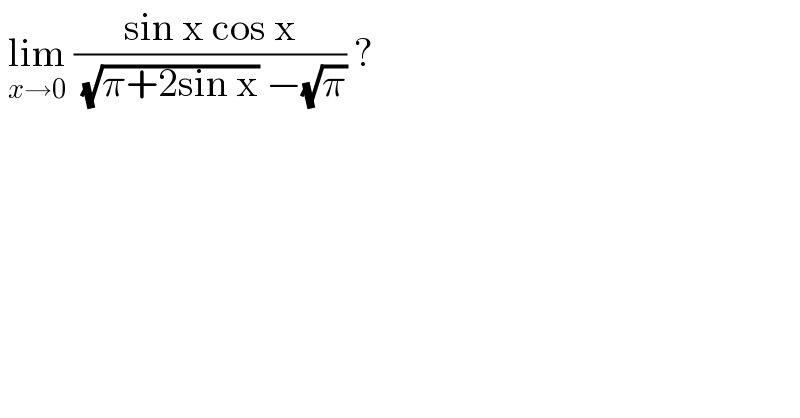
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\pi+\mathrm{2sin}\:\mathrm{x}}\:−\sqrt{\pi}}\:? \\ $$
Answered by Dwaipayan Shikari last updated on 09/Nov/20
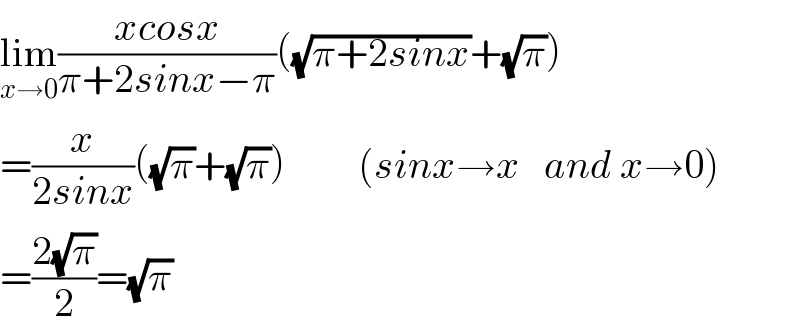
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{xcosx}}{\pi+\mathrm{2}{sinx}−\pi}\left(\sqrt{\pi+\mathrm{2}{sinx}}+\sqrt{\pi}\right) \\ $$$$=\frac{{x}}{\mathrm{2}{sinx}}\left(\sqrt{\pi}+\sqrt{\pi}\right)\:\:\:\:\:\:\:\:\:\left({sinx}\rightarrow{x}\:\:\:{and}\:{x}\rightarrow\mathrm{0}\right) \\ $$$$=\frac{\mathrm{2}\sqrt{\pi}}{\mathrm{2}}=\sqrt{\pi} \\ $$
Answered by liberty last updated on 09/Nov/20
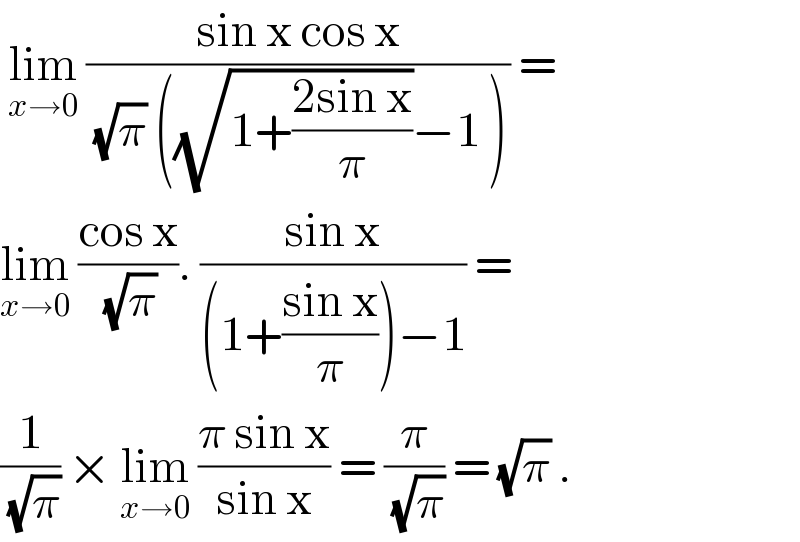
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:\mathrm{x}\:\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\pi}\:\left(\sqrt{\mathrm{1}+\frac{\mathrm{2sin}\:\mathrm{x}}{\pi}}−\mathrm{1}\:\right)}\:= \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:\mathrm{x}}{\:\sqrt{\pi}}.\:\frac{\mathrm{sin}\:\mathrm{x}}{\left(\mathrm{1}+\frac{\mathrm{sin}\:\mathrm{x}}{\pi}\right)−\mathrm{1}}\:=\: \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\pi}}\:×\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\pi\:\mathrm{sin}\:\mathrm{x}}{\mathrm{sin}\:\mathrm{x}}\:=\:\frac{\pi}{\:\sqrt{\pi}}\:=\:\sqrt{\pi}\:.\: \\ $$
