
Question Number 121449 by liberty last updated on 08/Nov/20
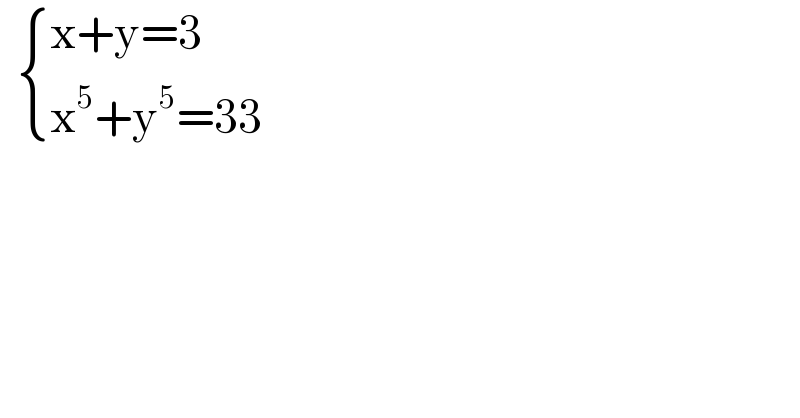
$$\:\:\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{3}}\\{\mathrm{x}^{\mathrm{5}} +\mathrm{y}^{\mathrm{5}} =\mathrm{33}}\end{cases} \\ $$
Commented by Dwaipayan Shikari last updated on 08/Nov/20
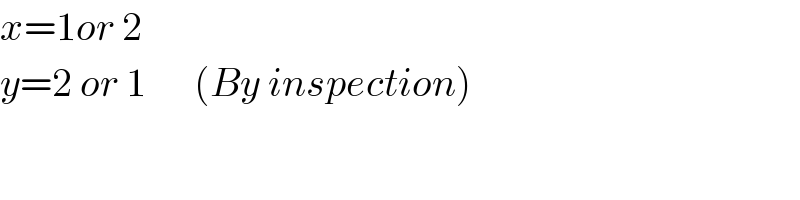
$${x}=\mathrm{1}{or}\:\mathrm{2} \\ $$$${y}=\mathrm{2}\:{or}\:\mathrm{1}\:\:\:\:\:\:\left({By}\:{inspection}\right) \\ $$
Answered by MJS_new last updated on 08/Nov/20
![x+y=a x^5 +y^5 =b let x=u−v∧y=u+v (1) 2u=a ⇒ u=(a/2) insert in (2) 5av^4 +((5a^3 )/2)v^2 +(a^5 /(16))=b v^4 +(a^2 /2)v^2 +((a^5 −16b)/(80a))=0 v=±(√(−(a^2 /4)±((√(5(a^5 +4b)))/(10(√a))))) [4 solutions] in this case u=(3/2)∧(v=±(1/2)∨v=±((√(19))/2)i)](Q121453.png)
$${x}+{y}={a} \\ $$$${x}^{\mathrm{5}} +{y}^{\mathrm{5}} ={b} \\ $$$$\mathrm{let}\:{x}={u}−{v}\wedge{y}={u}+{v} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{2}{u}={a}\:\Rightarrow\:{u}=\frac{{a}}{\mathrm{2}} \\ $$$$\mathrm{insert}\:\mathrm{in}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{5}{av}^{\mathrm{4}} +\frac{\mathrm{5}{a}^{\mathrm{3}} }{\mathrm{2}}{v}^{\mathrm{2}} +\frac{{a}^{\mathrm{5}} }{\mathrm{16}}={b} \\ $$$${v}^{\mathrm{4}} +\frac{{a}^{\mathrm{2}} }{\mathrm{2}}{v}^{\mathrm{2}} +\frac{{a}^{\mathrm{5}} −\mathrm{16}{b}}{\mathrm{80}{a}}=\mathrm{0} \\ $$$${v}=\pm\sqrt{−\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\pm\frac{\sqrt{\mathrm{5}\left({a}^{\mathrm{5}} +\mathrm{4}{b}\right)}}{\mathrm{10}\sqrt{{a}}}}\:\:\left[\mathrm{4}\:\mathrm{solutions}\right] \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$${u}=\frac{\mathrm{3}}{\mathrm{2}}\wedge\left({v}=\pm\frac{\mathrm{1}}{\mathrm{2}}\vee{v}=\pm\frac{\sqrt{\mathrm{19}}}{\mathrm{2}}\mathrm{i}\right) \\ $$
Commented by liberty last updated on 08/Nov/20

$$\mathrm{yes}.. \\ $$
Answered by bramlexs22 last updated on 08/Nov/20
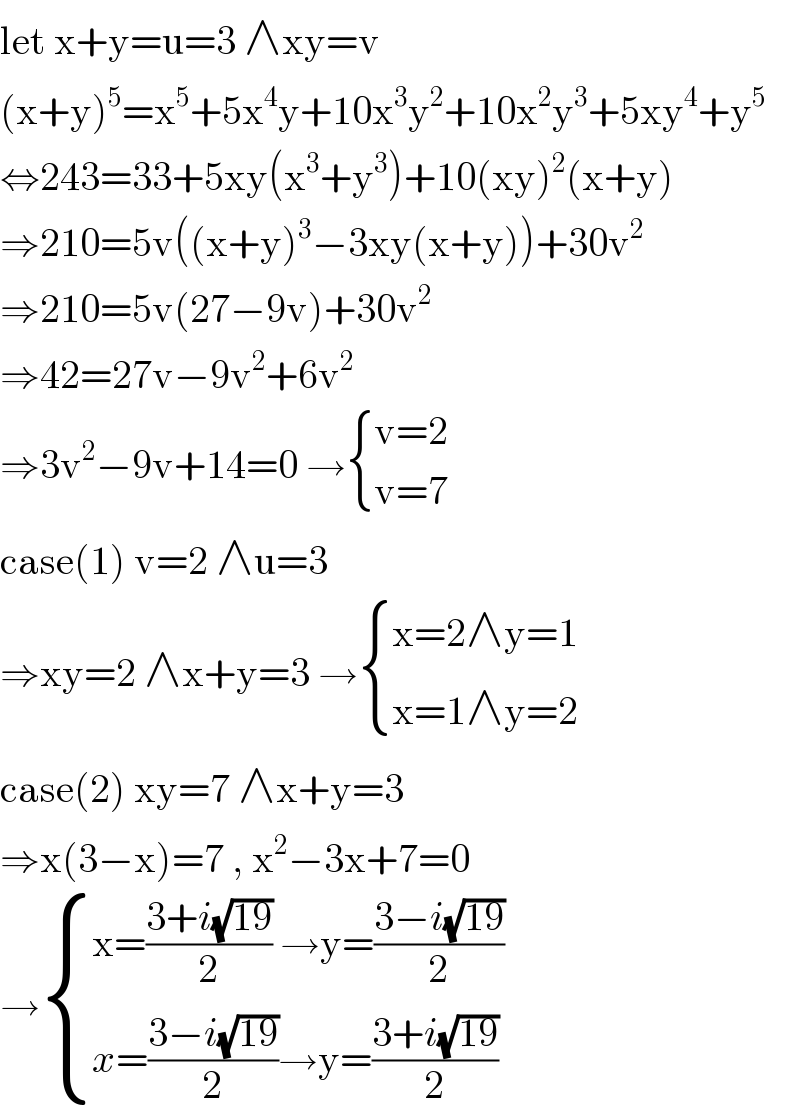
$$\mathrm{let}\:\mathrm{x}+\mathrm{y}=\mathrm{u}=\mathrm{3}\:\wedge\mathrm{xy}=\mathrm{v} \\ $$$$\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{5}} =\mathrm{x}^{\mathrm{5}} +\mathrm{5x}^{\mathrm{4}} \mathrm{y}+\mathrm{10x}^{\mathrm{3}} \mathrm{y}^{\mathrm{2}} +\mathrm{10x}^{\mathrm{2}} \mathrm{y}^{\mathrm{3}} +\mathrm{5xy}^{\mathrm{4}} +\mathrm{y}^{\mathrm{5}} \\ $$$$\Leftrightarrow\mathrm{243}=\mathrm{33}+\mathrm{5xy}\left(\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} \right)+\mathrm{10}\left(\mathrm{xy}\right)^{\mathrm{2}} \left(\mathrm{x}+\mathrm{y}\right) \\ $$$$\Rightarrow\mathrm{210}=\mathrm{5v}\left(\left(\mathrm{x}+\mathrm{y}\right)^{\mathrm{3}} −\mathrm{3xy}\left(\mathrm{x}+\mathrm{y}\right)\right)+\mathrm{30v}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{210}=\mathrm{5v}\left(\mathrm{27}−\mathrm{9v}\right)+\mathrm{30v}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{42}=\mathrm{27v}−\mathrm{9v}^{\mathrm{2}} +\mathrm{6v}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{3v}^{\mathrm{2}} −\mathrm{9v}+\mathrm{14}=\mathrm{0}\:\rightarrow\begin{cases}{\mathrm{v}=\mathrm{2}}\\{\mathrm{v}=\mathrm{7}}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{1}\right)\:\mathrm{v}=\mathrm{2}\:\wedge\mathrm{u}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{xy}=\mathrm{2}\:\wedge\mathrm{x}+\mathrm{y}=\mathrm{3}\:\rightarrow\begin{cases}{\mathrm{x}=\mathrm{2}\wedge\mathrm{y}=\mathrm{1}}\\{\mathrm{x}=\mathrm{1}\wedge\mathrm{y}=\mathrm{2}}\end{cases} \\ $$$$\mathrm{case}\left(\mathrm{2}\right)\:\mathrm{xy}=\mathrm{7}\:\wedge\mathrm{x}+\mathrm{y}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{x}\left(\mathrm{3}−\mathrm{x}\right)=\mathrm{7}\:,\:\mathrm{x}^{\mathrm{2}} −\mathrm{3x}+\mathrm{7}=\mathrm{0} \\ $$$$\rightarrow\begin{cases}{\mathrm{x}=\frac{\mathrm{3}+{i}\sqrt{\mathrm{19}}}{\mathrm{2}}\:\rightarrow\mathrm{y}=\frac{\mathrm{3}−{i}\sqrt{\mathrm{19}}}{\mathrm{2}}}\\{{x}=\frac{\mathrm{3}−{i}\sqrt{\mathrm{19}}}{\mathrm{2}}\rightarrow\mathrm{y}=\frac{\mathrm{3}+{i}\sqrt{\mathrm{19}}}{\mathrm{2}}}\end{cases} \\ $$
Commented by liberty last updated on 08/Nov/20

$$\mathrm{gave}\:\mathrm{kudos} \\ $$
Answered by mr W last updated on 08/Nov/20
![(x+y)^5 =x^5 +5x^4 y+10x^3 y^2 +10x^2 y^3 +5xy^4 +y^5 3^5 =33+5xy(x^3 +2x^2 y+2xy^2 +y^3 ) 3^5 =33+5xy[x^3 +3x^2 y+3xy^2 +y^3 −xy(x+y)] 3^5 =33+5xy[(x+y)^3 −xy(x+y)] 3^5 =33+5xy(3^3 −3xy) 14=xy(9−xy) (xy)^2 −9(xy)+14=0 (xy−2)(xy−7)=0 ⇒xy=2 or 7 z^2 −3z+2=0 ⇒(x,y)=1,2 z^2 −3z+7=0 ⇒(x,y)=((3+i(√(19)))/2),((3−i(√(19)))/2)](Q121458.png)
$$\left({x}+{y}\right)^{\mathrm{5}} ={x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} {y}+\mathrm{10}{x}^{\mathrm{3}} {y}^{\mathrm{2}} +\mathrm{10}{x}^{\mathrm{2}} {y}^{\mathrm{3}} +\mathrm{5}{xy}^{\mathrm{4}} +{y}^{\mathrm{5}} \\ $$$$\mathrm{3}^{\mathrm{5}} =\mathrm{33}+\mathrm{5}{xy}\left({x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} {y}+\mathrm{2}{xy}^{\mathrm{2}} +{y}^{\mathrm{3}} \right) \\ $$$$\mathrm{3}^{\mathrm{5}} =\mathrm{33}+\mathrm{5}{xy}\left[{x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{2}} {y}+\mathrm{3}{xy}^{\mathrm{2}} +{y}^{\mathrm{3}} −{xy}\left({x}+{y}\right)\right] \\ $$$$\mathrm{3}^{\mathrm{5}} =\mathrm{33}+\mathrm{5}{xy}\left[\left({x}+{y}\right)^{\mathrm{3}} −{xy}\left({x}+{y}\right)\right] \\ $$$$\mathrm{3}^{\mathrm{5}} =\mathrm{33}+\mathrm{5}{xy}\left(\mathrm{3}^{\mathrm{3}} −\mathrm{3}{xy}\right) \\ $$$$\mathrm{14}={xy}\left(\mathrm{9}−{xy}\right) \\ $$$$\left({xy}\right)^{\mathrm{2}} −\mathrm{9}\left({xy}\right)+\mathrm{14}=\mathrm{0} \\ $$$$\left({xy}−\mathrm{2}\right)\left({xy}−\mathrm{7}\right)=\mathrm{0} \\ $$$$\Rightarrow{xy}=\mathrm{2}\:{or}\:\mathrm{7} \\ $$$${z}^{\mathrm{2}} −\mathrm{3}{z}+\mathrm{2}=\mathrm{0}\:\Rightarrow\left({x},{y}\right)=\mathrm{1},\mathrm{2} \\ $$$${z}^{\mathrm{2}} −\mathrm{3}{z}+\mathrm{7}=\mathrm{0}\:\Rightarrow\left({x},{y}\right)=\frac{\mathrm{3}+{i}\sqrt{\mathrm{19}}}{\mathrm{2}},\frac{\mathrm{3}−{i}\sqrt{\mathrm{19}}}{\mathrm{2}} \\ $$
Commented by liberty last updated on 08/Nov/20

$$\mathrm{yess}... \\ $$
Commented by harckinwunmy last updated on 08/Nov/20

$$\mathrm{ff} \\ $$
