
Question Number 121444 by liberty last updated on 08/Nov/20
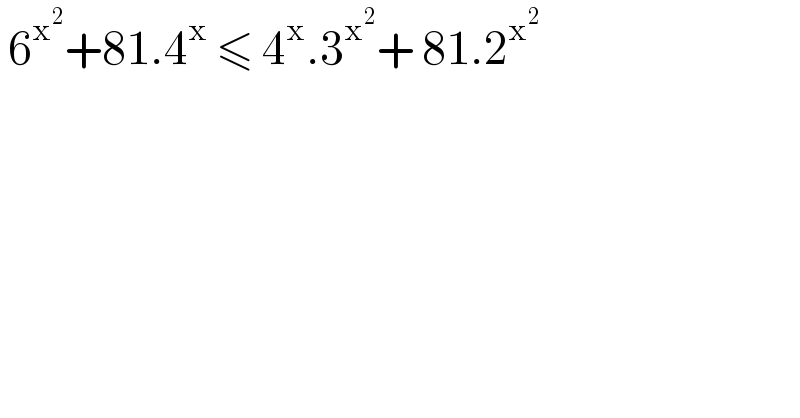
$$\:\mathrm{6}^{\mathrm{x}^{\mathrm{2}} } +\mathrm{81}.\mathrm{4}^{\mathrm{x}} \:\leqslant\:\mathrm{4}^{\mathrm{x}} .\mathrm{3}^{\mathrm{x}^{\mathrm{2}} } +\:\mathrm{81}.\mathrm{2}^{\mathrm{x}^{\mathrm{2}} } \\ $$
Commented by MJS_new last updated on 08/Nov/20
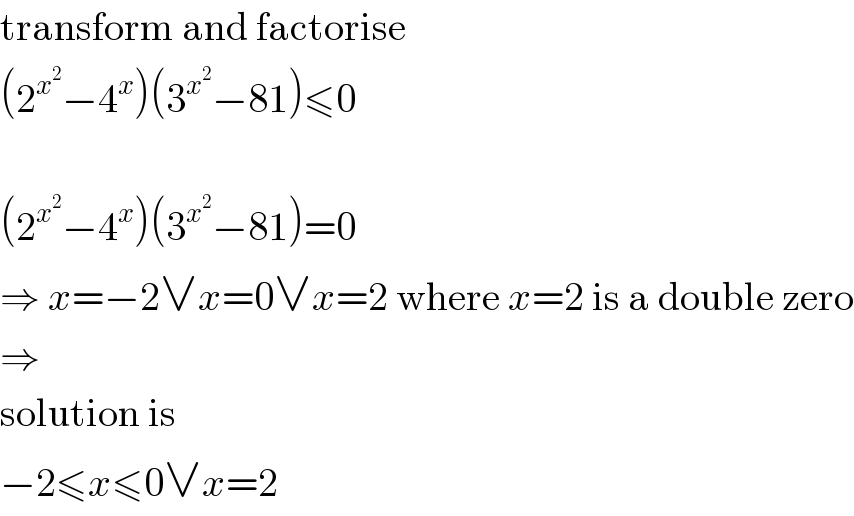
$$\mathrm{transform}\:\mathrm{and}\:\mathrm{factorise} \\ $$$$\left(\mathrm{2}^{{x}^{\mathrm{2}} } −\mathrm{4}^{{x}} \right)\left(\mathrm{3}^{{x}^{\mathrm{2}} } −\mathrm{81}\right)\leqslant\mathrm{0} \\ $$$$ \\ $$$$\left(\mathrm{2}^{{x}^{\mathrm{2}} } −\mathrm{4}^{{x}} \right)\left(\mathrm{3}^{{x}^{\mathrm{2}} } −\mathrm{81}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{x}=−\mathrm{2}\vee{x}=\mathrm{0}\vee{x}=\mathrm{2}\:\mathrm{where}\:{x}=\mathrm{2}\:\mathrm{is}\:\mathrm{a}\:\mathrm{double}\:\mathrm{zero} \\ $$$$\Rightarrow \\ $$$$\mathrm{solution}\:\mathrm{is} \\ $$$$−\mathrm{2}\leqslant{x}\leqslant\mathrm{0}\vee{x}=\mathrm{2} \\ $$
Commented by liberty last updated on 08/Nov/20

$$\mathrm{greatt} \\ $$
Commented by harckinwunmy last updated on 08/Nov/20

$$\mathrm{ff} \\ $$
