
Question Number 121201 by Ar Brandon last updated on 05/Nov/20

Commented by Ar Brandon last updated on 06/Nov/20

Commented by MJS_new last updated on 06/Nov/20

$$\mathrm{I}\:\mathrm{get}\:\mathrm{2}/\mathrm{2}/\mathrm{1}/\mathrm{3}\:\mathrm{solutions} \\ $$$${Ar}\:\:{Br}\:\:{Ct}\:\:{Dq} \\ $$
Commented by MJS_new last updated on 06/Nov/20

$${B}\:\mathrm{is}\:\mathrm{a}\:\mathrm{special}\:\mathrm{case}\:\mathrm{because}\:\mathrm{at}\:{x}=\mathrm{0}\:\mathrm{both} \\ $$$$\mathrm{logarithms}\:\mathrm{are}\:\mathrm{complex}\:\mathrm{but}\:\mathrm{the}\:\mathrm{imaginary} \\ $$$$\mathrm{part}\:\mathrm{cancels}\:\mathrm{out}.\:\mathrm{strictly}\:\mathrm{real}\:\mathrm{calculation} \\ $$$$\mathrm{leads}\:\mathrm{to}\:\mathrm{only}\:\mathrm{one}\:\mathrm{solution} \\ $$
Commented by Ar Brandon last updated on 06/Nov/20
Thanks Sir. For D after solving I had 3 solutions then rejected 3–√2 making them 2 solutions. Did you notice that too ? Or I made the mistake ?
Commented by liberty last updated on 06/Nov/20
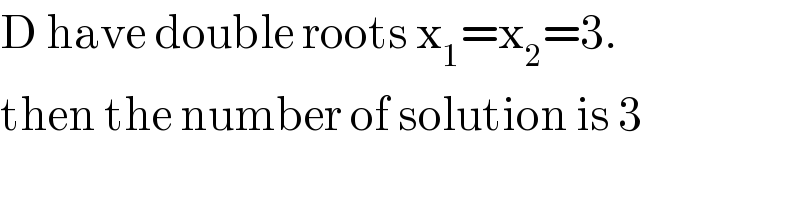
$$\mathrm{D}\:\mathrm{have}\:\mathrm{double}\:\mathrm{roots}\:\mathrm{x}_{\mathrm{1}} =\mathrm{x}_{\mathrm{2}} =\mathrm{3}. \\ $$$$\mathrm{then}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{3} \\ $$
Commented by MJS_new last updated on 06/Nov/20
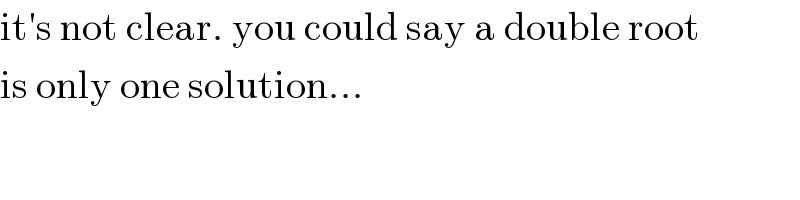
$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{clear}.\:\mathrm{you}\:\mathrm{could}\:\mathrm{say}\:\mathrm{a}\:\mathrm{double}\:\mathrm{root} \\ $$$$\mathrm{is}\:\mathrm{only}\:\mathrm{one}\:\mathrm{solution}... \\ $$
Answered by liberty last updated on 06/Nov/20
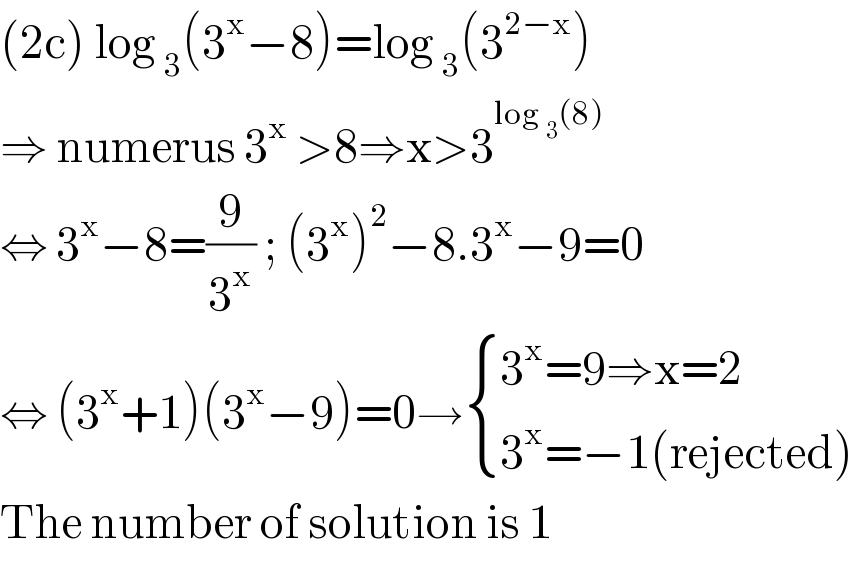
$$\left(\mathrm{2c}\right)\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{3}^{\mathrm{x}} −\mathrm{8}\right)=\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{3}^{\mathrm{2}−\mathrm{x}} \right) \\ $$$$\Rightarrow\:\mathrm{numerus}\:\mathrm{3}^{\mathrm{x}} \:>\mathrm{8}\Rightarrow\mathrm{x}>\mathrm{3}^{\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{8}\right)} \\ $$$$\Leftrightarrow\:\mathrm{3}^{\mathrm{x}} −\mathrm{8}=\frac{\mathrm{9}}{\mathrm{3}^{\mathrm{x}} }\:;\:\left(\mathrm{3}^{\mathrm{x}} \right)^{\mathrm{2}} −\mathrm{8}.\mathrm{3}^{\mathrm{x}} −\mathrm{9}=\mathrm{0} \\ $$$$\Leftrightarrow\:\left(\mathrm{3}^{\mathrm{x}} +\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{x}} −\mathrm{9}\right)=\mathrm{0}\rightarrow\begin{cases}{\mathrm{3}^{\mathrm{x}} =\mathrm{9}\Rightarrow\mathrm{x}=\mathrm{2}}\\{\mathrm{3}^{\mathrm{x}} =−\mathrm{1}\left(\mathrm{rejected}\right)}\end{cases} \\ $$$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{1} \\ $$
Answered by liberty last updated on 06/Nov/20
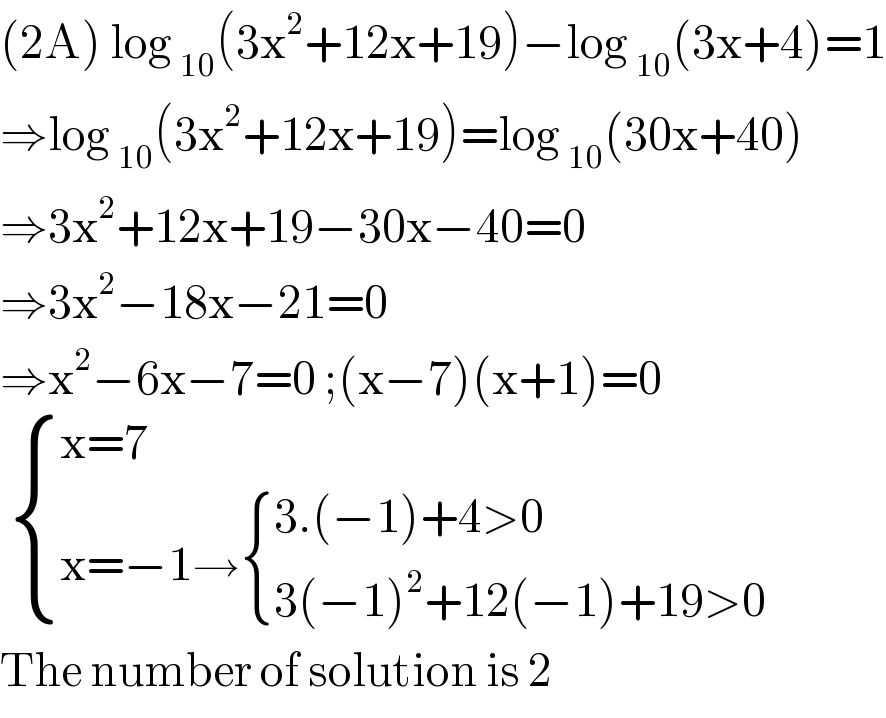
$$\left(\mathrm{2A}\right)\:\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{3x}^{\mathrm{2}} +\mathrm{12x}+\mathrm{19}\right)−\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{3x}+\mathrm{4}\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{3x}^{\mathrm{2}} +\mathrm{12x}+\mathrm{19}\right)=\mathrm{log}\:_{\mathrm{10}} \left(\mathrm{30x}+\mathrm{40}\right) \\ $$$$\Rightarrow\mathrm{3x}^{\mathrm{2}} +\mathrm{12x}+\mathrm{19}−\mathrm{30x}−\mathrm{40}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{3x}^{\mathrm{2}} −\mathrm{18x}−\mathrm{21}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} −\mathrm{6x}−\mathrm{7}=\mathrm{0}\:;\left(\mathrm{x}−\mathrm{7}\right)\left(\mathrm{x}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\:\begin{cases}{\mathrm{x}=\mathrm{7}}\\{\mathrm{x}=−\mathrm{1}\rightarrow\begin{cases}{\mathrm{3}.\left(−\mathrm{1}\right)+\mathrm{4}>\mathrm{0}}\\{\mathrm{3}\left(−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{12}\left(−\mathrm{1}\right)+\mathrm{19}>\mathrm{0}}\end{cases}}\end{cases} \\ $$$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{2}\: \\ $$
Answered by liberty last updated on 06/Nov/20
![(2D)2log _3 (x−2)+log _3 (x−4)^2 =0 numerus { ((x>2)),((x≠4)) :} ⇔ x∈(2,4) ∪(4,∞) ⇒log _3 (x−2)^2 +log _3 (x−4)^2 =0 ⇒log _3 [(x−2)(x−4)]^2 = log _3 (1) ⇒[(x−2)(x−4)]^2 =1 ⇒(x^2 −6x+8)^2 −1=0 ⇒(x^2 −6x+9)(x^2 −6x+7)=0 { (((x−3)^2 =0⇒x=3 ←double roots)),((x=((6±(√(36−28)))/2)=((6±2(√2))/2)=3±(√2))) :} 3+(√2) 4.414214 3−(√2) (rejected) 1.585786 The number of solution is 3](Q121210.png)
$$\left(\mathrm{2D}\right)\mathrm{2log}\:_{\mathrm{3}} \left(\mathrm{x}−\mathrm{2}\right)+\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{numerus}\:\begin{cases}{\mathrm{x}>\mathrm{2}}\\{\mathrm{x}\neq\mathrm{4}}\end{cases}\:\Leftrightarrow\:\mathrm{x}\in\left(\mathrm{2},\mathrm{4}\right)\:\cup\left(\mathrm{4},\infty\right) \\ $$$$\Rightarrow\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{x}−\mathrm{4}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{log}\:_{\mathrm{3}} \left[\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{4}\right)\right]^{\mathrm{2}} =\:\mathrm{log}\:_{\mathrm{3}} \left(\mathrm{1}\right) \\ $$$$\Rightarrow\left[\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}−\mathrm{4}\right)\right]^{\mathrm{2}} =\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{8}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{9}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{6x}+\mathrm{7}\right)=\mathrm{0} \\ $$$$\begin{cases}{\left(\mathrm{x}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0}\Rightarrow\mathrm{x}=\mathrm{3}\:\leftarrow\mathrm{double}\:\mathrm{roots}}\\{\mathrm{x}=\frac{\mathrm{6}\pm\sqrt{\mathrm{36}−\mathrm{28}}}{\mathrm{2}}=\frac{\mathrm{6}\pm\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{2}}=\mathrm{3}\pm\sqrt{\mathrm{2}}}\end{cases} \\ $$$$\mathrm{3}+\sqrt{\mathrm{2}} \\ $$$$\mathrm{4}.\mathrm{414214} \\ $$$$\mathrm{3}−\sqrt{\mathrm{2}}\:\left(\mathrm{rejected}\right)\: \\ $$$$\mathrm{1}.\mathrm{585786} \\ $$$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{3} \\ $$
Commented by Ar Brandon last updated on 06/Nov/20
Thanks�� Please can you have a look at the answers suggested by the book ?
Commented by Ar Brandon last updated on 06/Nov/20
There seem to be some contradictions I think. I too got some answers similar to yours but later on I had some doubts due to these contradictions
