
Question Number 121175 by Ar Brandon last updated on 05/Nov/20

Answered by MJS_new last updated on 05/Nov/20

$${x}<\mathrm{1} \\ $$$${g}\left({x}\right)<\mathrm{1} \\ $$
Commented by Ar Brandon last updated on 05/Nov/20
Any calculations or explanations, Sir ?��
Commented by MJS_new last updated on 05/Nov/20
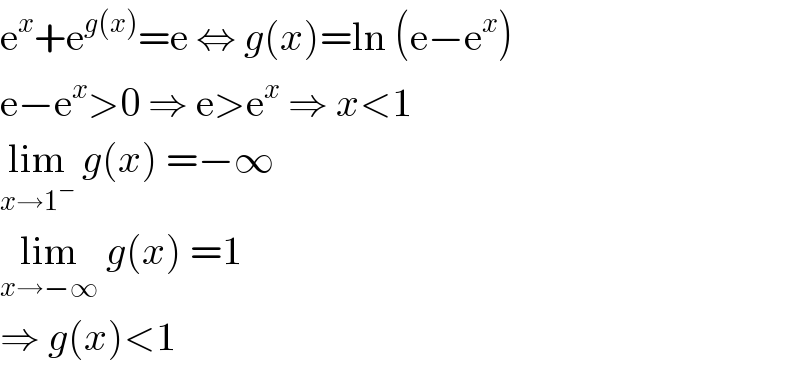
$$\mathrm{e}^{{x}} +\mathrm{e}^{{g}\left({x}\right)} =\mathrm{e}\:\Leftrightarrow\:{g}\left({x}\right)=\mathrm{ln}\:\left(\mathrm{e}−\mathrm{e}^{{x}} \right) \\ $$$$\mathrm{e}−\mathrm{e}^{{x}} >\mathrm{0}\:\Rightarrow\:\mathrm{e}>\mathrm{e}^{{x}} \:\Rightarrow\:{x}<\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{1}^{−} } {\mathrm{lim}}\:{g}\left({x}\right)\:=−\infty \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{g}\left({x}\right)\:=\mathrm{1} \\ $$$$\Rightarrow\:{g}\left({x}\right)<\mathrm{1} \\ $$
Commented by Ar Brandon last updated on 05/Nov/20
It's clear now. Thanks Sir
Commented by MJS_new last updated on 05/Nov/20

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
